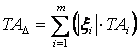Методические указания по выполнению курсовой работы по дисциплине «Взаимозаменяемость, стандартизация и технические измерения», страница 22

                                                  (7.7)

б) по вероятностному методу

                                    (7.8)

4. Определение допуска составляющего эвена при решении прямой задачи способом равных допусков:

а) по методу максимума-минимума

                                                              (7.9)

б) по вероятностному методу

                                              (7.10)

5. Определение среднего коэффициента точности при решении прямой задачи способом равной точности:

а) по методу максимума-минимума

                                                                (7.11)

б)         по вероятностному методу

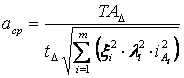                                        (7.12)

6.         Определение предельных отклонений по среднему отклонению:

а) для замыкающего эвена

                                                      (7.14)

б) для составляющего звена

                                                       (7.15)

                                                      (7.I6)

в) для корректирующего звена

                                                      (7.17)

                                                      (7.18)

3.7.3. Последовательность выполнения расчета

3.7.3.1. Решение прямой задачи,

1. Метод максимума-минимума:

а) составляется векторная схема, выявляются увеличивающие и уменьшающие составляющие звенья, а также замыкающее звено;

б) определяется допуск и координата середины поля допуска замыкающего эвена по известным предельным отклонениям:

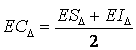                                                   (7.19)

в) распределяется допуск исходного (замыкающего) звена между составляющими звеньями:

способом равных допусков по формуле (7.9). При решении этим способом допуски всех составляющих звеньев принимаются одинаковыми:

Зная, что 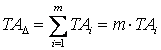 получим

где m     - число составляющих звеньев.

Способ равных допусков рекомендуется для предварительного назначения допусков составляющих размеров с последующей их корректировкой или в тех размерных цепях, где составляющие раз­меры одного порядка и могут быть получены с примерно одинако­вой экономической точностью;

способом одной степени точности (квалитета)   по формуле(7.11)

При этом способе решения принимают для всех составляющих звеньев допуски одной степени точности (равных квалитетов). Известно, что , следовательно, допуски одной степени точности имеют одинаковые коэффициенты точности:

, из зависимости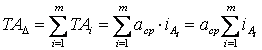 

получим:  

где    х - единица допуска для размера составляющего звена , мкм