Конспект лекций по дисциплине "Технологические основымашиностроения", страница 14

2)  по оси ординат откладывают абсолютную частоту (т/п, где m - число за­
готовок одного размера; п - общее число заготовок в партии).

Поскольку в пределах каждого интервала находятся детали с разными разме­рами, то для построения точек кривой определяют среднее арифметическое значе­ние данного интервала и из найденной точки восстанавливают перпендикуляр. По­сле соединения точек получают ломаную линию, которая называется кривой рас­пределения.

При нормальном ходе техпроцесса полученная кривая рассеивания случайных погрешностей приближается к кривой нормального распределения (кривой Гаусса), уравнение которой имеет вид:

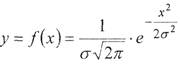
где у - частота появления погрешностей; σ - среднее квадратичное отклонение, рав­ное квадратному корню из средней арифметической суммы квадратов всех отклоне­ний; е - основание натурального логарифма е=2,718; х - отклонение действительных размеров от средних, равное разности размера каждой детали и среднего арифметического размера, то есть:

где L_i - фактический размер для каждой из деталей партии; L_cp. - средний размер де­талей партии.

При дискретном (прерывном) значении полученных размеров деталей в зоне рассеивания средний размер детали в партии равен среднему арифметическому из размеров деталей всей партии, то есть:

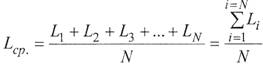
где L₁, L₂, L₃, …L_N - размеры деталей; N- число деталей в партии.

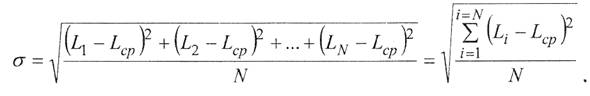
Среднее квадратичное отклонение определяют по формуле

Значение среднего квадратичного отклонения является единственным параметром , определяющим форму кривой нормального распределения. На схеме показаны кривые нормального распределения, ординаты которых определены при σ = 1;1,5; 2

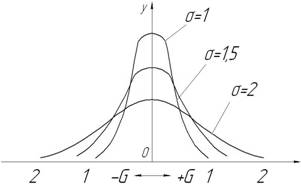
Рис. 3.1 Закон (кривая) Гаусса

Форма кривых позволяет сделать вывод, что чем меньше величина среднего квадратичного отклонения размеров, тем меньше кривая растянута, и, следователь­но, меньше рассеивание размеров. Таким образом, величина а определяет рассеива­ние размеров и характеризует степень влияния случайных погрешностей на точ­ность обработки.

Установлено, что в интервалах:

1)  x = ±0,36σ находится 35 % всех размеров обработанных деталей;

2)  х = ±0,76σ находится 50 % всех размеров обработанных деталей;

3)  х = ±3σ находится 99,7 % всех размеров обработанных деталей.

В последнем случае (х = ±3σ) кривая нормального распределения практически сливается с осью абсцисс, то есть отклонения действительных размеров от среднего размера для всех деталей находится в пределах ± Зσ или по абсолютной величине в пределах 6σ.

Отсюда вывод: если допуск δ на обработку заготовок больше 6σ, то точность техпроцесса соответствует требованиям (δ>6σ), Если допуск δ на обработку заготовок меньше 6σ, то часть деталей не соответствует требуемым размерам, то есть принятый техпроцесс механообработки неприемлем (δ<6σ).

Исследования с помощью математической статистики позволяют:

1)  определить точность технологического процесса (критерий точности условие δ≥6σ;

2)  определить вероятность получения числа деталей с размерами в интервале для допуска; для этого определяют относительную частоту появления погрешностей, то есть вероятность случаев у` абсолютной частоты у на число деталей в партии N, то есть