Конспект лекций по дисциплине "Аналитическая геометрия", страница 9

Следовательно, гипербола симметрична относительно обеих координатных осей.

При у = 0   х² = а²    х = ± а. Вершинами гиперболы будут точки А₁ (а; 0);    А₂ (-а; 0).

. В силу симметрии исследование ведем в I четверти

1) при   у  имеет мнимое значение, следовательно, точек гиперболы с абсциссами  не существует

2) при х = а; у = 0 А₁ (а; 0) принадлежит гиперболе

3) при x > a; y > 0. Причем при неограниченном возрастании х ветвь гиперболы уходит в бесконечность.

Отсюда следует, что гипербола представляет собой кривую, состоящую из двух бесконечных ветвей.

п 6. Асимптоты гиперболы

Рассмотрим вместе с уравнением  уравнение прямой

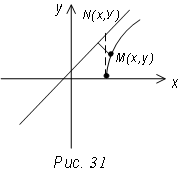Кривая будет лежать ниже прямой (рис. 31). Рассмотрим точки N (x, Y) и М (х, у) у которой абсциссы одинаковы, а У - у = MN. Рассмотрим длину отрезка MN

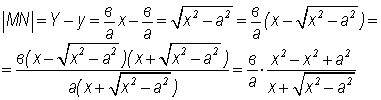
Найдем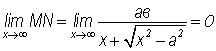

Итак, если точка М, двигаясь по гиперболе в первой четверти удаляется в бесконечность, то ее расстояние от прямой  уменьшается и стремится к нулю.

В силу симметрии таким же свойством обладает прямая .

Определение. Прямые к которым при  кривая неограниченно приближается называются асимптотами.

Итак, уравнение асимптот гиперболы .

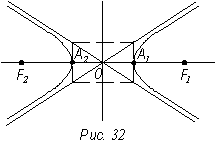
Асимптоты гиперболы располагаются по диагоналям прямоугольника, одна сторона которого параллельна оси ох и равна 2а, а другая параллельна оси оу и равна 2в, а центр лежит в начале координат (рис. 32).

п 7. Эксцентриситет и директрисы гиперболы

r₂ – r₁ = ± 2a      знак + относится к правой ветви гиперболы

                           знак – относится к левой ветви гиперболы

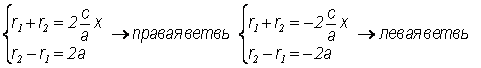
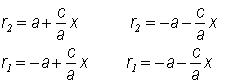
Определение. Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к расстоянию между ее вершинами.

. Так как c > a,  ε > 1

Выразим фокальные радиусы гиперболы через эксцентриситет:

Определение. Назовем прямые , перпендикулярные фокальной оси гиперболы и расположенными на расстоянии  от ее центра директрисами гиперболы, соответствующие правому и левому фокусам.

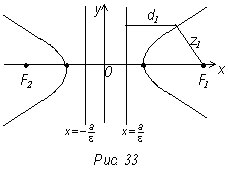Так как для гиперболы  следовательно, директрисы гиперболы, располагаются между ее вершинами (рис. 33). Покажем, что отношение расстояний любой точки гиперболы до фокуса и соответствующей директрисы есть величина постоянная и равная ε.