Конспект лекций по дисциплине "Аналитическая геометрия", страница 7

М (х, у) – текущая точка окружности (рис. 26). Тогда по формуле расстояние между двумя точками имеем:

 или

(х - а)² + (у - в)² + R²           (1) => уравнение окружности

Если центр окружности совпадает с началом координат, то ее уравнение имеет вид:       х² + у² = R²            (2)

 или

 или

      (1^|)

где

Итак, уравнение окружности – есть уравнение II степени

Вывод: Но не всякое уравнение II степени есть окружность. Чтобы уравнение II степени определяло окружность нужно, чтобы коэффициенты при х² и у² были одинаковы, а член с произведением ху должен отсутствовать.

п. 3 Эллипс и его каноническое уравнение

Определение. Эллипсом называется геометрическое место точек , сумма расстояний которых до двух данных точек (F₁ и F₂) , называемых фокусами есть величина постоянная.

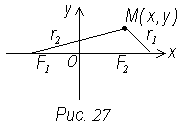
Для вывода уравнения эллипса выберем систему координат ХОУ, чтобы фокусы эллипса F₁ и F₂ лежали на оси абсцисс, а начало координат делило бы расстояние между фокусами пополам (рис. 27)

Обозначим F₁ F₂ = 2c

Тогда F₁ (c, 0); F₂ (-c; 0).

Возьмем произвольную точку М (х, у), лежащую на эллипсе, тогда MF₁ = r₁, MF₂ = r₂. Числа r_r и r₂ называются фокальными радиусами эллипса.

Согласно определению эллипса r₁ + r₂ = const.

Обозначим ее через 2а.

Тогда r₁ + r₂ = 2a; F₁ F₂ = 2c, отсюда a > c

Упростим это выражение, избавившись от иррациональности

Обозначим а² – с² = в², тогда х²в² + у²а² = а²в² делим почленно на а²в²

 каноническое уравнение эллипса

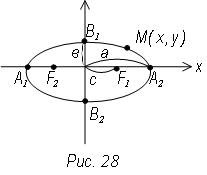
Так как уравнение эллипса содержит х и у в четных степенях, то если точка М (х, у) находится на эллипсе, то и точки с координатами М₁ (х; -у), М₂ (-х; -у), М₃ (-х; -у) тоже находятся на эллипсе. Следовательно, оси координат являются осями симметрии эллипса.

Ось симметрии, на которой расположены фокусы называются фокальной осью.

Точки пересечения эллипса с осями симметрии называются вершинами.

Найдем координаты вершин эллипса при

Следовательно вершинами эллипса будут точки с координатами А₁ (а; 0);  А₂ (-а; 0); В₁ (0; в); В₂ (0; -в).

Отрезок А₁А₂ – большая ось эллипса

               В₁В₂ – малая ось эллипса

а – большая полуось; в – малая полуось