Конспект лекций по дисциплине "Аналитическая геометрия", страница 3

В аналитической геометрии всякую линию можно рассматривать как геометрическое место точек как геометрического места точек. В определении линии, как геометрического места точек содержится свойство общее всем ее точкам.

Возьмем на плоскости какую-нибудь линию и рассмотрим  произвольную точку указанной линии. Если точка будет перемещаться по данной линии, то ее координаты х и у будут меняться, оставаясь, однако связанным некоторым условием, характеризующим точки данной линии. Таким образом, мы получим некоторое соотношение между Х и У, которое выполняется только при движении точки по линии и нарушается, если точка сойдет с линии.

Следовательно, линии на плоскости соответствует некоторое уравнение с двумя переменными Х и У.

Определение. Уравнением данной линии называется такое уравнение     F (x, y) = 0 c двумя переменными, которому удовлетворяют координаты х и у каждой точки, лежащей на этой линии, и не удовлетворяют координатам никакой точки, не лежащей на ней.

Определение. Линия, определенная уравнением вида y = f (x) называется графиком функции y = f (x).

Поскольку величины Х и У рассматриваются как координаты переменной точки, их называют текущими координатами.

п 2. Примеры заданий линий при помощи уравнений

Уравнение y = f (x) между координатами х и у определяют линию как геометрическое место тех точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры

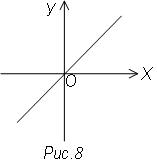
1) х – у = 0; у = х Геометрическое место точек, для которых абсцисса равна ординате, представляет собой биссектрису I и III координатных углов (рис. 8).

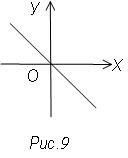
2) у + х = 0       у = -х

Геометрическое место точек представляет биссектрису II и IV координатных углов (рис. 9).

Если левая часть уравнения F (x, y) = 0 раскладывается на множители, то приравнивая к нулю каждый множитель отдельно, получим несколько уравнений

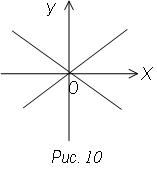
3) х² – у² = 0     (х - у)(х + у) = 0

х + у = 0     х – у = 0

Уравнение, определяет пару прямых (биссектрисы координатных углов) (рис. 10)

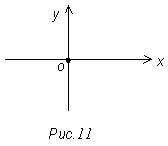
4) х² + у² = 0 представляет собой одну точку (начало координат) (рис. 11)

5) х² +у² + 2 = 0;  х² + у² = -2 не определяет никакого геометрического места точек.

п 3. Получение линии как геометрического места точек

Дана линия как геометрическое место точек. Требуется составить уравнение этой линии.

Если линия определена как геометрическое место точек, подчиненных известному условию, то, выражая эти условия при помощи координат, мы получим некоторую зависимость между координатами. Это и будет уравнением этой линии.

Чтобы составить уравнение линии как геометрического места точек, обладающих заданным свойством нужно:

1) взять произвольную (текущую точку М (х, у) линии

2) записать равенством общее свойство всех точек линии

3) входящие в равенство отрезки выразить через текущие координаты точки М (х, у) и через данные задачи4) упростить полученное уравнение и определить вид кривой.

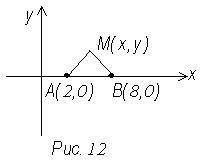Пример: вывести уравнение траектории точки М, которое в каждый момент движения находится вдвое ближе к точке А (2, 0) чем к точке В (8, 0) (рис. 12)

Решение: