Конспект лекций по дисциплине "Аналитическая геометрия", страница 12

Выделим полный квадрат

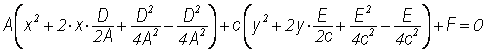
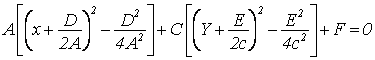
Перенесем начало координат в точку

Тогда по формуле (1а)

 обозначим

Получим         (4)

Рассмотрим различные случаи

I А и В одного знака (всегда можно сделать А > 0 В > 0)

1) U > 0  Поделим (4)  почленно на U, тогда

  Получим уравнение эллипса, его центр имеет координаты

, а оси параллельны координатным осям

2)  - это уравнение определяет одну точку, для которой  или

3) U < 0 правая часть уравнения (4) отрицательна и нет ни одной точки, удовлетворяющей этому уравнению (т.е. оно не определяет ни какой линии)

II. А и С разных знаков Пусть А > 0; C < 0

1)  U > 0 разделим уравнение (4) на U

 → уравнение гиперболы, имеющей действительную ось , а мнимую ось

3)

Пусть A = m²,   c = - n²

Это уравнение распадается на два уравнения первой степени

Каждое из них проходит через точку,  т.е. через точку .

III. С = 0, Е ≠ 0 Выделим полный квадрат

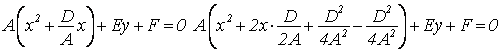
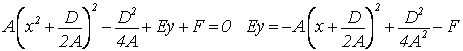
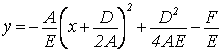
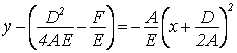
Обозначим               

Тогда у – в = к (х - а)²

Перенесем начало координат в точку

Полагая

Тогда мы получим уравнение параболы. Ее вершина находится в точке , а осью симметрии является ось  параллельная оси оу.

2)  Е = 0 имеем Ax² +Dx + F = 0 пусть x₁ и х₂ корни этого характеристического уравнения, тогда А (х - х₁) (х – х₂) = 0

Мы получили два уравнения первой степени х = х₁ и х = х₂. т.е. получили уравнения двух прямых параллельных оси оу (т.е парабола выродилась в пару параллельных прямых), а если х₁ = х₂, то они сливаются в одну.

Если уравнение Ах² + Dx + F не имеет действительных корней, то нет ни одной точки, которая удовлетворяла бы заданному уравнению.

п 5. Преобразование общего уравнения второго порядка

Рассмотрим общее уравнение второй степени

Ax² +Bxy +Cy² + Dx + Ey + F = 0      где   В ≠ 0

Покажем, что при помощи поворота координатных осей его всегда можно привести к виду не содержащему члена с произведением переменных.