Конспект лекций по дисциплине "Аналитическая геометрия", страница 2

или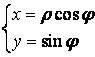  –  формулы, выражающие декартовы координаты через полярные.

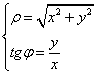  –  формулы, выражающие полярные координаты через декартовы.

§ 2 Простейшие задачи аналитической геометрии на плоскости

п 1. Проекция отрезка на оси координат

Определение. Прямая, на которой выбрано положительное направление, называется осью (рис. 4).

 Определение. Отрезок АВ называется направленным, если сказано, какая из точек считается началом отрезка, какая концом. Направлением отрезка считается направление от начала к концу .

Рассмотрим произвольный отрезок .  (рис. 5)

Пусть А₁ и В₁ – основания перпендикуляров, опущенных из начала и конуса отрезка АВ на ось х.

А₂ и В₂ – основания перпендикуляров, опущенных из начала и конца от отрезка АВ на ось у. В нашем случае направление отрезка А₁ В₁ совпадает с положительным направлением оси ох. Направление отрезка А₂ В₂ противоположному направлению оси оу.

Определение. Число, равное разности х₂ -  х₁ назовем проекцией отрезка АВ на ось ох и обозначим символом

Определение. Число, равное разности у₂ – у₁ назовем проекцией отрезка АВ на ось оу и обозначим символом

т.е. проекции отрезка на ох равно разности абсцисс конца и начала отрезка, а проекции отрезка на ось оу равна разности ординат конца и начала от резка.

В нашем случае

п 2 .Расстояние между двумя точками на координатной плоскости

Расстояние между двумя точками обычно обозначаются буквой d (d>0).

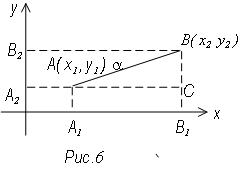Пусть А (х₁, у₁) и В (х₂, у₂) начало и конец отрезка АВ (рис. 6)

Опустим из А и В перпендикуляры на координатные оси из Δ АВС

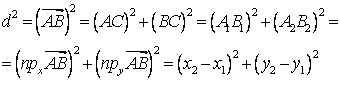
п 3. Деление отрезка в данном отношении

Пусть А (х₁, у₁) – начало, а В (х₂, у₂) конец отрезка АВ. Пусть точка С делит отрезок АВ в отношении λ. Требуется найти х_с и у_с – координаты точки С (рис. 7)

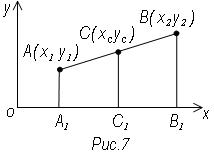Пусть

Опустим из А, В, С перпендикуляры на ось ох. АА₁, ВВ₁, СС₁ - параллельные прямые, поэтому они отсекают на отрезке АВ и оси х т. Пропорциональные отрезки т.е.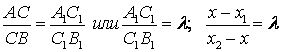

или  

Если точка С (х₀, у₀) – середина отрезка АВ, то  и

§ 3 Линии и их уравнения

п 1. Понятие уравнения линии

В элементарной геометрии достаточно исследуются лишь немногие линии: прямая, окружность, ломанная. Между тем потребности техники ставят перед математикой общую задачу исследования многочисленных линий, многообразных по своей форме и характеру своих свойств. Для решения этой задачи, требуется более совершенные методы. Такие методы дают алгебры и математический анализ. В основе применения методов алгебры и анализа лежит общий способ задания линии при помощи ее уравнения.