Конспект лекций по дисциплине "Аналитическая геометрия", страница 5

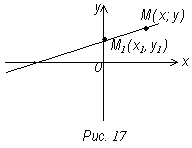
Возьмем на прямой произвольную точку М (х, у)

Тогда 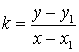 или   y –y₁ = k(x – x₁)

п 4. Уравнение прямой, проходящей через две точки

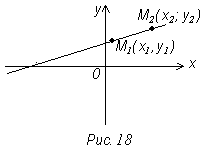Пусть даны две точки прямой М₁ и М₂ (рис. 18).

Тогда 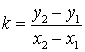. Подставим k в предыдущее равенство

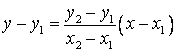  или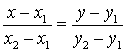

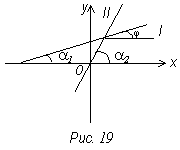п 5. Угол между двумя прямыми

Определение. Угол между прямыми (I) и (II) называется угол на который нужно повернуть прямую I, чтобы она совпала со II.

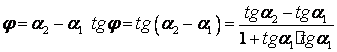
или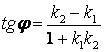

п 6 Условие параллельности и перпендикулярности двух прямых

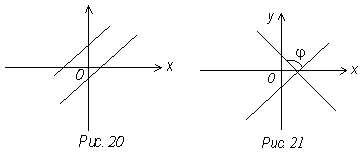Если прямые параллельны, то φ = 0   tg φ = 0    k₂ – k₁ = 0

k₂ = k₁

Если прямые перпендикулярны, то φ = 90⁰

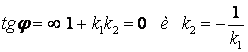
п 7 Прямая как линия первого порядка. Общее уравнение прямой

Теорема. В декартовых координатах каждая прямая определяется уравнением первого порядка и обратно, каждое уравнение первой степени определяет некоторую прямую.

ДОКАЗАТЕЛЬСТВО

1). Пусть дана произвольная прямая. Если она не перпендикулярна оси ох, то ее уравнение имеет вид y = kx + b; это есть уравнение I степени.

Если прямая перпендикулярна оси ох и отсекает на ней отрезок, то ее уравнение имеет вид:  х = а тоже уравнение I степени.

2). Дано уравнение первой степени АХ + ВУ +С = 0. Покажем, что оно определяет прямую.

Пусть В ≠ 0, тогда  обозначим

Получим у = kx + b – уравнение прямой

Если В = 0, то  есть уравнение прямой

Вывод. Каждая прямая линия I –го порядка и обратно каждая линия       I –го порядка есть прямая.

Определение. Уравнение AX + DY + C = 0 называется общим уравнением прямой.

п 8. Уравнение прямой в отрезках

Пусть дано уравнение Ах + Ву + С = 0 и пусть А ≠ 0; В ≠ 0; С ≠ 0.

Ах + Ву = - С поделим почленно на – С

 

Получим     уравнение прямой в отрезках

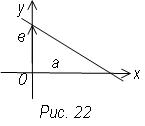
а и b  отрезки, которые, прямая отсекает на координатных осях ох и оу

при у = 0    х = а;       при х = 0  у = b

п 9. Нормальное уравнение прямой

Дана прямая. Проведем через начало координат нормаль  к прямой.

Р – точка пересечения нормали и прямой.

На нормали зададим положительное направление от точки О к точке Р.

Обозначим через Р длину отрезка ОР (рис. 23).

α – угол между нормалью и положительным направлением оси ох.