Конспект лекций по дисциплине "Аналитическая геометрия", страница 13

Повернем координатные оси на угол α. Тогда согласно формуле (2) имеем

Подставим х и у в исходное уравнение

Выберем угол α таким, чтобы коэффициент  равнялся нулю

Т.е.   или

Делим на sin2α

       (5)

Таким образом, всегда можно выбрать угол α таким, чтобы после поворота осей на этот угол в уравнении исчезает член с произведением ху. Угол α будем выбирать так чтобы .

Пример упростить уравнение

.    Согласно формуле (2)

    Подставляем х и у в исходное уравнение

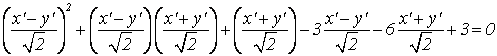
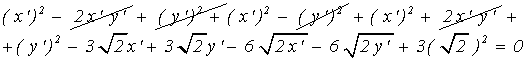
или   выделяемый полный квадрат

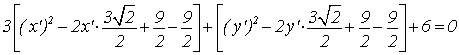
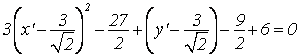
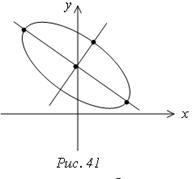Мы получили эллипс с полуосями  координаты центра в системе координат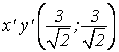

Найдем координаты эллипса в системе хоу (рис. 41)

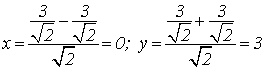
Рекомендуемая литература

1. Привалов И.И. Аналитическая геометрия. М. Наука 1964 г.

2. Ефимов Н.В. Краткий курс аналитической геометрии. М. Наука 1985 г.

3. Александров А.С. Лекции по аналитической геометрии. М. Наука 1968 г.

                            Моисеенко Сергей Степанович

Аналитическая геометрия на плоскости

КОНСПЕКТ ЛЕКЦИЙ

направление 6.070104 «Морской и речной транспорт»

Тираж -  ____ экз.   Подписано к печати ___. ____. ______

Заказ №  _____   Объем _____ п.л.

Издательство «Керченский государственный морской технологический университет»

98309, г.Керчь, ул.Орджоникидзе, 82