Конспект лекций по дисциплине "Аналитическая геометрия", страница 6

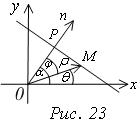
Возьмем на прямой произвольную точку М (х, у)  (рис 23). Обозначим через Р длину отрезка ОР (рис. 23).

Α – угол между нормально и положительным направлением оси ох.

Возьмем на прямой произвольную точку М (х, у) .

  отсюда   или  - нормальное уравнение прямой

п. 10. Расстояние от точки до прямой

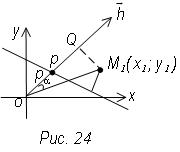Пусть дана прямая и точка вне ее (рис. 24).

Определение.  Отклонением точки М₁ от данной прямой назовем число td, если точка М, и начало координат лежат по разные  стороны от прямой и число –d, если прямая и точка М₁ лежат по одну сторону от начала координат.

Но     отсюда

Пусть дано общее уравнение прямой Ах + Ву + С = 0 (1) и нормальное уравнение этой прямой        (2)

Так как уравнения  (1) и(2) определяют одну и туже прямую, то коэффициенты этих уравнений пропорциональны. Это означает, что умножив все числа уравнения (1)  на одно и тоже число μ мы получим уравнение (2)

                                                                 

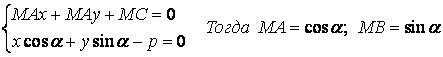
Число μ называется  нормирующим множителем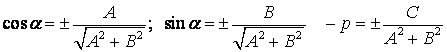

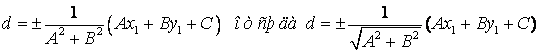
или 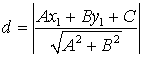 - формула расстояния от точки до прямой

п. 11. Уравнение прямой в полярных координатах

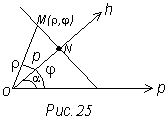Положение прямой линии на плоскости вполне определено, если задать расстояние р полюса и угла α между полярной осью и нормалью  к прямой

пр  или

      => уравнение прямой, в полярных координатах.

§ 5 Кривые второго порядка

п.1 Общее уравнение II степени

Общее уравнение II степени относительно переменных х и у может содержать члены второй степени х²; у²; ху первой степени х; у и свободный член.

Общее уравнение II степени имеет вид:

Ах² +Вху +Су² +Дх + Fy + E = 0

где, по крайней мере, один из коэффициентов отличен от нуля.

Мы рассмотрим следующие кривые второго порядка: окружность, эллипс, гиперболу, параболу.

п 2. Окружность

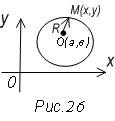Определение. Окружностью называется геометрическое место точек равноудаленных от одной точки, называемой центром окружности.

 Выведем уравнение окружности.

Пусть точка О (а, в) – центр окружности. R ее радиус.