Конспект лекций по дисциплине "Аналитическая геометрия", страница 8

п.4 Эксцентриситет и директрисы эллипса

Определение. Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине его большой оси.

 так как с < a, то ε< 1

Так как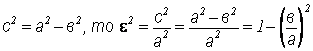

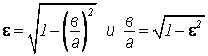
Эксцентриситет характеризует форму эллипса. Чем ближе ε к единице, тем меньше  и тем сильнее вытянут эллипс.

Чем ближе ε к нулю, тем меньше вытянут эллипс. Для окружности ε = 0 .

Выразим фокальные радиусы эллипса через эксцентриситет

 имеем

итак

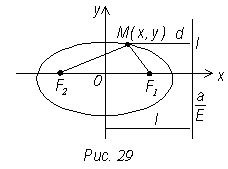Рассмотрим прямую параллельную оси у (рис. 29). Расстояние d₁ от произвольной точки эллипса до прямой равно:

r₁ = a - . Поделим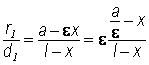

Пусть ; тогда

То есть соотношение  сохраняет постоянное значение. В силу симметрии тоже заключение можно сделать относительно левого фокуса F₂ и прямой с уравнением .

Определение. Две прямые, перпендикулярные к фокальной оси эллипса и отстоящие на расстоянии   от его центра называются директрисами эллипса.

Свойство директрис: отношение расстояний любой точки эллипса до фокуса и соответствующей директрисы есть величина постоянная и          равная .

§ 5. Гипербола и ее каноническое уравнение

Определение. Гиперболой называется геометрическое место точек, разность от каждой из которых до двух данных точек, называемых фокусами есть величина постоянная

Возьмем систему координат, так чтобы фокусы лежали на оси абсцисс, а начало координат делило отрезок F₁ F₂ пополам   (рис. 30). Обозначим F₁ F₂ = 2c. Тогда F₁ (с; 0);          F₂ (-c; 0)

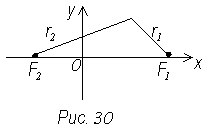MF₂ = r₂, MF₁ = r₁ – фокальные радиусы гиперболы.

Согласно определения гиперболы r₁ – r₂ = const.

Обозначим ее через 2а

Тогда r₂- r₁ = ±2a итак:

 => каноническое уравнение гиперболы

Так как уравнение гиперболы х и у в четных степенях, то если точка          М₀ (х₀; у₀) лежит на гиперболе, то на ней лежат также точки М₁ (х₀; -у₀)               М₂ (-х₀; -у₀) М₃ (-х₀; -у₀).