![]()
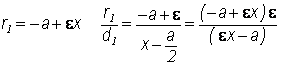
п. 8 Парабола и ее уравнение
 Определение. Парабола есть геометрическое
место точек равностоящих от данной точки, называемой фокусом и от данной прямой
называемой директрисой.
Определение. Парабола есть геометрическое
место точек равностоящих от данной точки, называемой фокусом и от данной прямой
называемой директрисой.
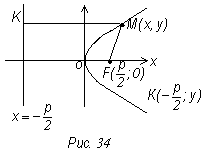
Чтобы составить уравнение параболы примем за ось х
прямую, проходящую через фокус F1 перпендикулярную
к директрисе и будем считать ось х направленной от директрисы к фокусу. За
начало координат возьмем середину О отрезка от точки F до данной прямой,
длину которого обозначим через р (рис. 34). Величину р назовем
параметром параболы. Точка координат фокуса ![]() .
.
Пусть М (х, у) – произвольная точка параболы.
Согласно определению ![]()
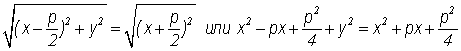 у2
= 2рх – каноническое уравнение параболы
у2
= 2рх – каноническое уравнение параболы
Для определения вида параболы преобразуем ее уравнение
![]() отсюда следует
отсюда следует ![]() . Следовательно, вершина параболы
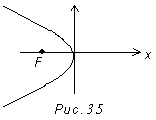
находится в начале координат и осью симметрии параболы является ох. Уравнение у2
= -2рх при положительном р сводится к уравнению у2 = 2рх путем
замены х на –х и ее график имеет вид (рис. 35).
. Следовательно, вершина параболы
находится в начале координат и осью симметрии параболы является ох. Уравнение у2
= -2рх при положительном р сводится к уравнению у2 = 2рх путем
замены х на –х и ее график имеет вид (рис. 35).
 Уравнение х2 = 2ру является уравнением параболы
с вершиной в точке О (0; 0) ветви которой направлены вверх.
Уравнение х2 = 2ру является уравнением параболы
с вершиной в точке О (0; 0) ветви которой направлены вверх.
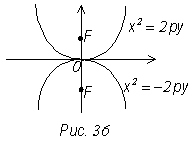 х2 = -2ру – уравнение параболы с центром в
начале координат симметричная относительно оси у, ветви которой направлены вниз
(рис. 36).
х2 = -2ру – уравнение параболы с центром в
начале координат симметричная относительно оси у, ветви которой направлены вниз
(рис. 36).
У параболы одна ось симметрии.
Если х в первой степени, а у во второй, то ось симметрии есть х.
Если х во второй степени, а у в первой, то ось симметрии есть ось оу.
Замечание 1. Уравнение директрисы параболы имеет вид ![]() .
.
Замечание 2.Так как для параболы ![]() , то ε параболы
равен 1. ε = 1.
, то ε параболы
равен 1. ε = 1.
 п. 9 Уравнение эллипса,
гиперболы и параболы в полярных координатах
п. 9 Уравнение эллипса,
гиперболы и параболы в полярных координатах
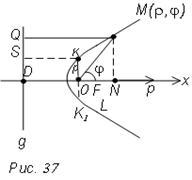
Пусть дана одна из названных линий (L). Пусть F – фокус линии, g – соответствующая этому фокусу директриса. Введем полярную систему координат, так чтобы фокус совпадал с полюсом, а полярную ось направим в сторону противоположную директрисе, перпендикулярной ее (рис. 37).
Возьмем произвольную точку М (ρ, φ) на линии L.
Возьмем соотношение ![]() (1). В нашем случае r = ρ
(1). В нашем случае r = ρ
d = MQ = DF + FN = DF + ρ cosφ. Проведем фокальную хорду КК' (КК' перпендикулярно фокальной оси).
Пусть KF = р (фокальный параметр)
Вследствие (1) ![]()
Отсюда ![]() , то
, то 
![]() - полярное
уравнение кривой второго порядка.
- полярное
уравнение кривой второго порядка.
§ 6. Преобразование координат
п. 1 Преобразование координат при параллельном сдвиге осей
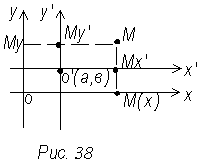 Пусть ох и оу старые, а o|x| и o|у| новые координатные оси
ох|
Пусть ох и оу старые, а o|x| и o|у| новые координатные оси
ох| ![]() ох; оу|
ох; оу| ![]() оу (рис. 38)
оу (рис. 38)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.