Конспект лекций по дисциплине "Аналитическая геометрия", страница 4

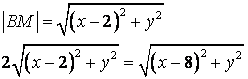
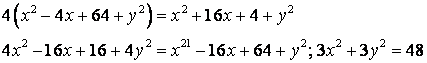
 - уравнение окружности

п 4. Параметрические уравнения линий

В некоторых случаях при составлении уравнения линий текущие координаты не связаны одним уравнением, а каждую координату в отдельности выражают в виде функции нового переменного, например t и получают уравнения вида:

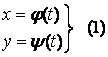
Условные величины Х и У для каждого значения t рассматривать как координаты некоторой точки М. При изменении t величины Х и У меняются, следовательно точка М перемещается по плоскости.

Равенства (1) называются параметрическими уравнениями траектории    точки М; аргумент t называется переменным параметром.

Параметрические уравнения играют важную роль в механики, где они используются в качестве уравнений движения. Параметр t играет в этом случае роль времени.

Если из уравнений (1) исключить параметр t, то получим уравнение между Х и У вида F (x, y) = 0

Пример 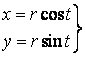  исключить параметр t

               

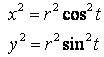
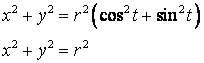
Получим уравнение окружности с центром в начале координат.

п 5. Алгебраические линии

Определение. Уравнение F (x, y) называется алгебраическим, если выражение F (x, y) есть сумма конечного числа слагаемых вида, где k и m - целые неотрицательные числа. А – действительное число.

При этом наибольшая из степеней k + m называется степенью уравнения

х + у – 5   - уравнение 1-й степени;

ху + 7 - х + 4у   - уравнение 2-й степени

х³у⁴ – у²х + 3 = 0  - уравнение 7-й степени

Общий вид уравнения 1-й степени Ах + Ву + С = 0

Общий вид уравнения 2-й степени

Ах² + Вху +Су² + Dx + Fy + F = 0

У нас линии 1-го и 2-го порядка

§ 4 Прямая на плоскости

п 1. Угловой коэффициент

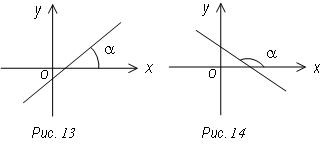α – угол наклона прямой к положительному направлению оси ох.

Определение. Тангенс угла наклона прямой к положительному направлению оси ох называется угловым коэффициентом этой прямой.

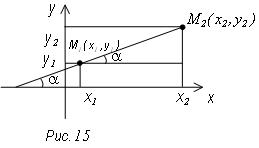
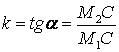 или 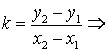 эта формула выражает угловой коэффициент прямой по двум ее точкам.

п 2. Уравнение прямой с угловым коэффициентом

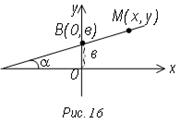Пусть дана некоторая прямая. Выведем уравнения данной прямой, полагая известным ее угловой коэффициент k и величину b – направленного отрезка , который она отсекает на оси у (рис. 15).

Выберем текущую точку прямой М (х,у)         (рис. 16) и точку В (о; b)

 отсюда у = kx + b  уравнение прямой с угловым коэффициентом

п 3. Уравнение прямой, проходящей через данную точку М₁ (х₁; у₁)

и заданным угловым коэффициентом