Пусть положение новых осей относительно старой системы определяется заданием старых координат нового начала o| (а, в)
а – величина сдвига по направлению оси ох
в – величина сдвига по направлению оси оу.
Произвольная точка М имеет относительно старых осей координат М (х, у) относительно новых М (x| , у|).
Наша цель установить формулы, выражающие х и у через x| , у| и наоборот.
Спроектируем точку М на оси ох и o|x|.
ОМх = о o|х + o|хМх или х = x| + а (1) → выражение старых координат
аналогично у = у| + в через новые
x| = х – а (1 а) выражение новых координат
у| = у – в через старые
п 2. Преобразование декартовых прямоугольных координат при повороте осей
 Пусть ох и оу – старые,
а ох| и оу| - новые координатные оси. Положение новых осей
относительно старых определяется заданием угла поворота, совмещающих старые оси
с новыми (рис. 39).
Пусть ох и оу – старые,
а ох| и оу| - новые координатные оси. Положение новых осей
относительно старых определяется заданием угла поворота, совмещающих старые оси
с новыми (рис. 39).Пусть α – угол поворота. Произвольная точка М имеет относительно старых осей координаты х; у, а относительно новых x|; у|. Наша цель установить формулы, выражающие х и у через x| и у и обратно.
Пусть ρ и φ полярные координаты точки М, если за полярную ось принять ось ох и ρφ', если за полярную ось принять оx'
![]()
Отсюда ![]()
![]()
Итак, ![]() → выражение старых координатных
осей через новые.
→ выражение старых координатных
осей через новые.
Формулы, выражающие новые координаты x' и y' через старые х и y'. Можно получить из следующих рассуждений.
Если новая система получается из старой путем поворота на угол α, то старая система получается из новой путем поворота на угол – α. Поэтому в равенствах (2) можно поменять местами старые и новые координаты, заменяя одновременно α на – α.
Тогда: ![]()
или ![]() (2а) → выражение
новых координатных осей через старые.
(2а) → выражение
новых координатных осей через старые.
п 3. Преобразование декартовых координат при изменении начала и поворота осей
Пусть а – величина сдвига в направлении оси ох; в – величина сдвига в направлении оси оу α – угол поворота
 х, у
координаты точки М в старых осях
х, у
координаты точки М в старых осях
x'; y' – координаты точки М в новых осях (рис. 40).
Введем вспомогательную
систему координат ![]() , направление осей которой
совпадает с направлением осей старой системы, а начало координат совпадает с
началом новой системы.
, направление осей которой
совпадает с направлением осей старой системы, а начало координат совпадает с
началом новой системы.
Тогда согласно (1) ![]()
Согласно (2) ![]() тогда
тогда ![]()
Решим систему относительно x' и y'

![]()
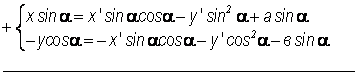
![]()
Итак ![]() (3а)
(3а)
п. 4 Преобразование общего уравнения второй степени не содержащего произведения переменных
Запишем общий вид такого
уравнения ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.