Особенности обеспечения пространственной жесткости многоэтажных гражданских зданий. Ветровые и сейсмические нагрузки. Расчетные модели диафрагмовых систем. Особенности проектирования надпроёмных перемычек ядер жесткости. Особенности проектирования пространственных несущих систем на основе каменной кладки, страница 9

                   Рис. 4.1

Если расположение диафрагм в плане здания не симметрично, то помимо изгиба в направлении соответствующих осей столбы системы подвергаются кручению.

Поворот плана здания не симметричной системы происходит относительно центра жесткости под действием крутящего момента  . Координаты центра жесткости относительно геометрического центра плана определится следующим образом

;          

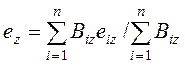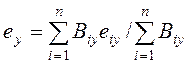
где e_z(y) – расстояние между центром жесткости и геометрическим центром плана;  – расстояние между центром тяжести сечения -ой диафрагмы, параллельной оси до геометрического центра плана здания вдоль оси .

Учитывая, что перекрытия считаются абсолютно жесткими в своей плоскости, перемещения отдельных диафрагм при повороте будут линейно зависимы. Тогда для линейно зависимых перемещений имеем

                  ,                                                                                       (*)

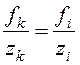где  – перемещения соответствующих диафрагм при повороте.

Принимая во внимание, что прогибы  и  прямо пропорциональны действующей нагрузке и обратно пропорциональны изгибной жесткости. Вместо условия (*) имеем

           ,                                                                                (**)

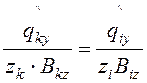где 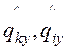 – доля внешней горизонтальной нагрузки, приходящейся на k-тую или i-тую диафрагму, возникающей при повороте плана здания.

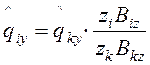         ;                                                                                   (4)

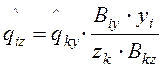        .                                                                                  (5)

Согласно условиям равновесия, интенсивность внешнего крутящего момента от горизонтальной нагрузки должен быть уравновешен внутренними моментами.    

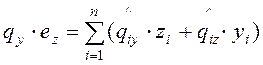          .                                                               (6)

Заменяя и  через  по формулам (4) и (5) получим

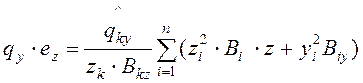          .                                               (7)

Нагрузка, приходящаяся на -тую диафрагму, параллельную оси , вызванную поворотом плана здания относительно центра жесткости будет равна

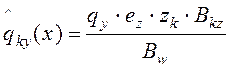                                                                                 (8)

где 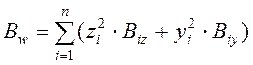 – жесткость диафрагмовой системы на кручение при изгибе.

Рассматривая совместно выражения (8), (1), и (2) можно определить полную нагрузку, приходящуюся на -тую диафрагму, если к фасаду здания приложена горизонтальная нагрузка интенсивностью  с эксцентриситетом относительно центра жесткости .

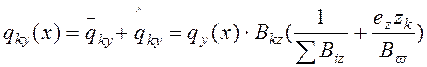.                                              (9)

          Нагрузка, приходящаяся на  диафрагму, параллельную оси , вызванную центральным действием силы  с эксцентриситетом  определяется следующим образом

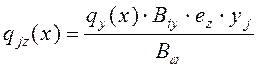.                                                                         (10)

Таким образом работой диафрагм в плоскости наименьшей жесткости при расчете несущей системы пренебрегают.

  Ось относительно которой работает диафрагма

Рис. 4.2.   Схема работы диафрагмы в плане.

Условие (9) получено для диафрагм параллельных оси  при действии горизонтальной нагрузки вдоль этой же оси.

Если рассмотреть диафрагмы, параллельные оси и нагрузку в этом же направлении, то в условии (9) можно заменить на,а на .

4.2. Расчет диафрагмовой системы на вертикальные

       нагрузки

        Пространственное деформирование диафрагмовой системы при действии вертикальных нагрузок возникает тогда, когда к отдельным элементам её приложены погонные моменты . Эти погонные моменты  и , действующие в отдельных диафрагмах создают полные моменты в сечении Х в плоскостях, параллельных осям У и Z:

          ;        .                                                                  (11)

          Если плоскости изгиба диафрагмовой системы от результирующих моментов , проходят через центр жесткости, то несущая система деформируется без кручения. Пространственное деформирование системы с изгибным кручением возникает при выполнении условия

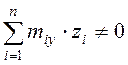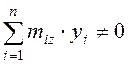                   ;       ,                                                          (12)