Особенности обеспечения пространственной жесткости многоэтажных гражданских зданий. Ветровые и сейсмические нагрузки. Расчетные модели диафрагмовых систем. Особенности проектирования надпроёмных перемычек ядер жесткости. Особенности проектирования пространственных несущих систем на основе каменной кладки, страница 23

11.2. Особенности проектирования тела ядра

         жесткости

Сборные ядра жесткости монтируются из колонн каркаса и стенок диафрагм. Возможно также компоновка ядер жесткости при отсутствии колонн каркаса.

Наиболее распространены монолитные ядра жесткости, возводимые в скользящей или переставной опалубке.

Ядро многоэтажного здания в общем случае подвергается изгибу в 2-х взаимно ортогональных вертикальных плоскостях, чистому кручению, изгибному кручению и сжатию.

В результате в стенках здания возникают нормальные s и касательные напряжения t, которые приводят к возникновению в наклонных сечениях главных растягивающих и главных сжимающих напряжений . Так как ядра чаще всего имеют проемы, то по высоте ядра жесткости можно выделить 2 характерных расчетных горизонтальных сечения: первое сечение - на участке без проёмов, высотой яруса h1 и второе сечение – на участке с проёмами высотой h2 (h2 равна высоте проёмов). Очевидно, что наиболее напряженными являются участки с проёмами. Для произвольного i-го столба, заключенного между соседними проемами, эти напряжения определяются по известным формулам внецентренного сжатия от действия усилий от действия сжимающих сил, изгибающих моментов и крутящего момента. При расчете усилия от изгиба и кручения определяются комплексно при деформировании ядра в целом в виде , , . При этом нормальные напряжения в j-той точке горизонтального сечения i-того столба определяется из условия

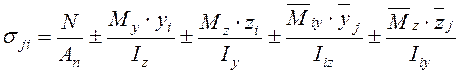,                                        (1)

где N – вертикальная расчетная нагрузка, собранная на данное ядро в соответствии с грузовыми площадями в рассматриваемом уровне; площадь горизонтального сечения ядра за вычетов проёмов; изгибающие моменты в соответствующих плоскостях, приходящиеся на данное ядро, определяются из общего статического расчета пространственной системы; момент инерции расчетного сечения ядра нетто относительно соответствующих осей, проходящих через центр тяжести этого ядра; коэффициенты центра тяжести -того столба относительно собственной центральной координатной системы данного ядра; моменты инерции -того столба относительно оси перпендикулярной плоскости изгиба данного столба и проходящие через центр тяжести этого столба; координаты -той точки столба, вычисляемые в собственной системе координат этого столба; изгибающие моменты в -том столбе от смещения ядра при его кручении, по направлениям каждой из осей равные:

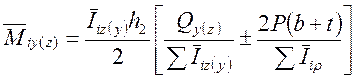,                                                          (2)

где поперечная сила, приходящаяся на рассчитываемое ядро в направлении y (z) от изгиба и изгибного кручения; сумма моментов инерции столбов диафрагм относительно собственных центральных осей, перпендикулярных плоскости изгиба; сумма моментов инерции всех столбов ядра относительно осей перпендикулярных направлению поворота, для угловых столбов ;  размеры сторон сечения ядра в плане в осях; , ; ; P – сдвигающая сила, вызванная чистым кручением, определяемая по формуле:

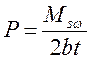                                              ,                                                         (3)

здесь момент чистого кручения, воспринимаемый сечением ядра.

Условие (3) вытекает из соотношения Бредта, если предположить, что поток касательных напряжений t, создаваемых кручением, равномерно распределен п*о толщине стенок ядра: 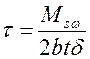, где толщина стенки ядра жесткости.

При получении зависимостей (2) предполагалось, что сдвигающее усилие  одинаково в соседних сечениях: сплошном и ослабленном проемами.

Максимальное, нормальное сжимающее напряжение определяется из условия (1) не должно превышать расчетного сопротивления бетона на сжатие     . Этим условием определяется необходимое количество вертикальной продольной арматуры в столбах ядра, поэтому в условии (1) и (2) геометрические характеристики столбов и всего ядра должны приниматься приведёнными с учетом наличия арматуры , ,   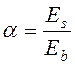. При этом площадь сечения арматуры принимается исходя из оптимального коэффициента армирования. Наибольшее нормальное растягивающее напряжение (1) не должно превышать расчетного сопротивления бетона растяжению , так как в теле ядра жесткости трещины не могут быть допущены из-за опасности их прогрессивного развития под влиянием знакопеременной горизонтальной нагрузки.