Особенности обеспечения пространственной жесткости многоэтажных гражданских зданий. Ветровые и сейсмические нагрузки. Расчетные модели диафрагмовых систем. Особенности проектирования надпроёмных перемычек ядер жесткости. Особенности проектирования пространственных несущих систем на основе каменной кладки, страница 7

В результате такой замены, при расчете больших систем алгебраических уравнений с большим количеством неизвестных заменяется одним диференциальным уравнением или системой диференциальных уравнений, порядок которых равен числу вертикальных швов между несущими вертикальными элементами.

          Разновидностью дискретно-континуальных моделей являются консольная и консольно-заменяющая модель.

          В консольной модели связи сдвига считаются либо шарнирными, либо абсолютно жесткими. Такая модель используется для расчета связевых каркасов, а при небольшой модификации и для расчета бескаркасных систем.

Рис. 3.7.  Консольно заменяющая модель диафрагмовой системы

В консольно-заменяющих моделях несущая система заменяется одним консольным стержнем, изгибная и сдвиговая жесткость которого эквивалентна аналогичным характеристикам всей системы.

Расчет по общей дискретно-континуальной модели достаточно сложен, поэтому в ней используются возможные упрощения. В частности симметричные в плане несущие системы разбиваются на 2 независимые плоскопараллельные поперечные и продольные несущие системы.

Кроме того, во всех моделях для удобства расчета начало вертикальной координаты несущей системы располагают в верхней точке здания, а ось направляют вниз.

Помимо моделей схематизации при расчете пространственных систем принимают следующие рабочие гипотезы:

1) плоские стенки диафрагм жесткости не испытывают сопротивления чистого кручения;

2) междуэтажные перекрытия считаются абсолютно жесткими в своей горизонтальной плоскости и абсолютно гибкими из неё;

3) в связях пренебрегают осевыми деформациями;

4) материал элементов несущей системы считается физически линейным;

5) считается, что при деформировании несущей системы её элементы получают малые перемещения.

3.2. Предварительный расчет количества диафрагм

      жесткости

Подбор необходимого количества диафрагм жесткости производится в 2-х взаимно-ортогональных направлениях. Этот выбор возможен только для несущих систем, близких к симметричным в плане, которые включают в себя диафрагмы близкие по изгибной и осевой жесткости, воспринимающие близкие по значению вертикальные нагрузки.

Если несущая система обладает ярко выраженной асимметрией, или в системе используются диафрагмы различной жесткости, то предварительный выбор количества диафрагм по сравнению с уточнённым расчетом вносит погрешность  30%.

В общем случае количество диафрагм, располагаемых параллельно одной из осей плана здания, ориентировочно задаётся из условия

        ,

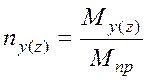где  – количество диафрагм параллельных оси y(z).

          z

               y

       Рис. 3.8

 – равнодействующий изгибающий момент от действия вертикальных и горизонтальных нагрузок, приложенных по всей несущей системе, и действующих в плоскости  и .

 – предельный допустимый момент, воспринимаемый одной диафрагмой жесткости.

Суммарный изгибающий момент, действующий на всю несущую систему, от внешних нагрузок в плоскости  или  устанавливается исходя из опыта проектирования по приближенной формуле

        ,                                           (1)

где  – консольный изгибающий момент, действующий на всю несущую систему в соответствующей плоскости от горизонтальной нагрузки

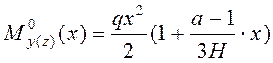        ,                                                                (2)

где  – интенсивность ветровой нагрузки в уровне верха здания;    – полная высота здания;  – коэффициент, учитывающий внецентренное приложение вертикальной нагрузки.

На первом этапе, когда неизвестны эксцентриситеты вертикальной нагрузки   .

Если же расположение диафрагм известно, и известны эксцентриситеты приложения вертикальной нагрузки, то вместо  следует принимать фактический момент от вертикальных и горизонтальных нагрузок, действующих на всю систему;  – суммарная нагрузка с учетом веса конструкции и временных нагрузок, собранная со всех этажей в пределах плана здания.

Предельно допустимый момент, действующий в одной диафрагме, определяется из условия ограничения горизонтального перемещения верха диафрагмы и назначается из условия