Особенности обеспечения пространственной жесткости многоэтажных гражданских зданий. Ветровые и сейсмические нагрузки. Расчетные модели диафрагмовых систем. Особенности проектирования надпроёмных перемычек ядер жесткости. Особенности проектирования пространственных несущих систем на основе каменной кладки, страница 10

где  и  считаются положительными, если они приводят к прогибу элементов несущей системы в направлении, противоположном направлению соответствующей оси.

          Рассуждая аналогично, как и для горизонтальной нагрузки, изгибающий момент в произвольном сечении диафрагмы вызванный действием внецентренно приложенной нагрузки с учетом закручивания здания определяется следующим образом

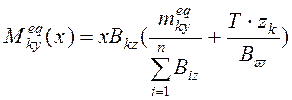                   ,                                                            (13)

где  – бимомент в пространственной несущей системе от внецентренно приложенных вертикальных нагрузок.

 

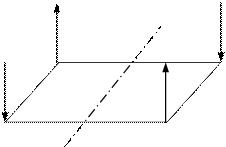                                        депланация сечений из своей плоскости

Рис. 4.3.  Схема депланации сечения из своей плоскости.

Поперечная сила, действующая в -той диафрагме, параллельной оси , зависит от того, приложен ли непосредственно к ней момент  или нет.

Если к столбу приложен момент , то поперечная сила, действующая в его сечении определяется следующим образом

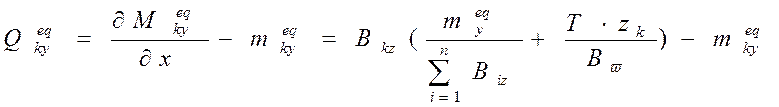
Если же в диафрагме непосредственно не действует момент , то поперечная сила для этого столба будет равна 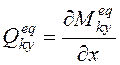. Возникновение дополнительного члена становится очевидным, если рассмотреть механику деформирования двух столбов, связанных шарнирно и загруженных внецентренной погонной вертикальной нагрузкой. Очевидно, что поперечные усилия от вертикальной нагрузки постоянны по высоте диафрагм, т. е. .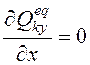

Внецентренное приложение вертикальной нагрузки к диафрагме возникает тогда, когда связями сдвига соединен столб диафрагм и элементы рамы с одной стороны, либо в случае пары смежных столбов. В этом случае возникает погонный момент .

Окончательно, в результате статического расчета на совместное действие вертикальных и горизонтальных нагрузок определяется распределение моментов и поперечных сил, а так же продольных усилий между отдельными диафрагмами

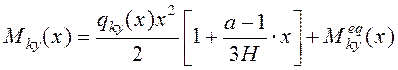                          ;                                  (14)

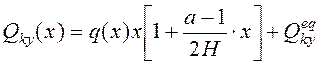                                    ;                                      (15)

                                    .                                                                    (16)

 

                     

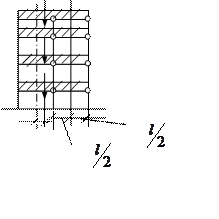
Рис. 4.4. Внецентренное приложение вертикальной нагрузки в случае

пары смежных столбов.

Горизонтальные перемещения диафрагмы, вызванные пространственным деформированием всей системы можно определить,  дважды проинтегрировав выражение момента (14) и поделить результат на жесткость -той диафрагмы :

   

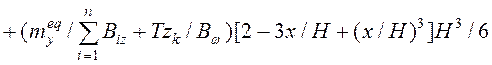               .                              (17)

Максимальный прогиб диафрагмы, возникающий в верхней точке здания, т.е. при :

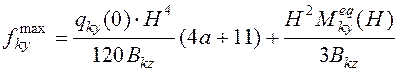              .                                               (18)

Максимальный момент диафрагмы, вызванный вертикальной и горизонтальной нагрузками, должен быть ограничен величиной

                                       .

Формулы (14) – (18) получены для горизонтальной нагрузки, приведенной к эквивалентной трапеции и для равномерного распределения моментов  по высоте. По этим формулам определяются расчетные характеристики и для направления вдоль оси Z при замене индексов У на Z и Z на У.

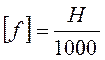Л Е К Ц И Я    № 5

П Л А Н

5.1. Особенности расчета ядро диафрагмовых систем

5.1. Особенности расчета ядро-диафрагмовых систем

Пространственные несущие системы, в состав которых входят не только плоские диафрагмы, но и пространственные стволы – ядра жесткости, называются ядро-диафрагмовыми системами.

Совместная деформация ядер и диафрагм обеспечивается жесткими дисками перекрытий. Если диафрагмы и ядра жесткости располагаются не симметрично в плане, то полное перемещение каждого из перекрытий складывается из поступательных смещений в направлении ортогональных осей и поворота относительно центра жесткости .

В общем случае ядро-диафрагмовые системы оказывают сопротивление изгибу, чистому кручению и изгибному кручению.

При расчете ядро-диафрагмовых систем помимо общепринятых гипотез считаются справедливыми следующие допущения:

1. Чистому кручению оказывают сопротивление только замкнутые ядра жесткости.