Особенности обеспечения пространственной жесткости многоэтажных гражданских зданий. Ветровые и сейсмические нагрузки. Расчетные модели диафрагмовых систем. Особенности проектирования надпроёмных перемычек ядер жесткости. Особенности проектирования пространственных несущих систем на основе каменной кладки, страница 13

,                                                                                                 (2)

где     ;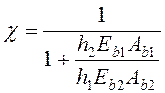

– высота стенки диафрагмы в пределах одного этажа.

Если конструкция монолитная, то .

При расчете диафрагмовых систем по консольной модели, ригели считаются шарнирно соединены со стенками, а связи, соединяющие элементы диафрагм по вертикальным швам, считаются абсолютно жесткими.

При переходе к дискретно-континуальной модели жесткость связей сдвига необходимо уточнить. Влияние податливости связей сдвига на деформативность и несущая способность диафрагмовой системы учитывается при помощи коэффициента условий работы, который определяется в результате и модельных испытаний систем, состоящих из однотипных диафрагм.

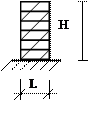Установлено, что влияние связей сдвига снижается при увеличении высоты здания.

         Коэффициент условия работы связей сдвига определяют по эмпирической формуле

       Рис. 6.1. 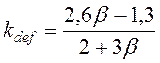                                     ,                                                (3)

где относительная высота столба диафрагм; высота всей диафрагмы; поперечный размер в направлении наибольшей жесткости; .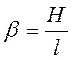

Окончательно приведенная жесткость сборной диафрагмы с учетом податливости вертикальных и горизонтальных швов определяется следующим образом

.

6.2. Учет податливости основания на деформирование

несущей системы

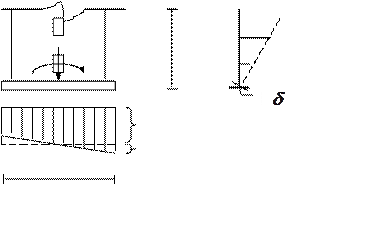
Горизонтальное смещение элементов диафрагм зависит от жесткости основания под фундаментами. В общем случае вертикальная продольная сила и момент в диафрагме под подошвой фундамента создают давление на грунт в виде трапециевидной эпюры.

Из этой эпюры можно выделить симметричную и кососимметричную составляющие.

Действие кососимметричной составляющей приводит к крену подошвы фундамента на угол .

Соответственно на этот же угол отклоняются стенки диафрагмы от вертикали (диафрагма жестко соединена с фундаментом).

 

                                                       

                                    

                       

                              

     L

Рис. 6.2. Эпюра напряжений в основании диафрагмы.

величина смещения края фундамента;

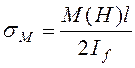        ,                                                                                      (4)

где размер фундамента в направлении наибольшей жесткости; момент инерции площади подошвы фундамента; момент в уровне верхнего обреза фундамента.

Учитывая, что перемещения малы, а следовательно мал угол крена , его величину можно вычислить

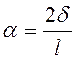         .                                                                                                 (5)

Величина вертикальной осадки  определяется в зависимости от коэффициента пастели ().

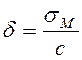        ;                                                                                                (6)

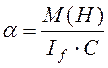        ;                                                                                          (5’)

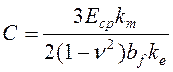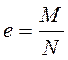где ; средний модуль деформаций и коэффициент Пуассона грунта в пределах сжимающей толщи грунта, принимаются по СНиП2.02.01-83*;   – ширина подошвы фундамента, перпендикулярной направлению его крена; коэффициент, определяемый по таблице СНиП2.02.01-83* в зависимости от направления крена, формы фундамента и величины эксцентриситета ; коэффициент определяемый по СНиП в зависимости от  и .

В произвольной по высоте диафрагме плоскости горизонтальные перемещения можно определить геометрически из простых геометрических соображений

Максимальный прогиб диафрагмы, вызванный податливостью основания при должен быть ограничен величиной

,

где полная высота.

Такой же величиной ограничивается прогиб диафрагмы от действия горизонтальной и вертикальной нагрузок.

6.3. Учет продольного изгиба на деформации и усилия

      диафрагмовой системы

При действии вертикальных внецентренно приложенных нагрузок прогибы элементов диафрагм системы увеличиваются, а следовательно и возрастают начальные эксцентриситеты приложения этих вертикальных сил, что ведёт к повышению результирующего момента, поперечной силы и горизонтальным деформациям.