Особенности обеспечения пространственной жесткости многоэтажных гражданских зданий. Ветровые и сейсмические нагрузки. Расчетные модели диафрагмовых систем. Особенности проектирования надпроёмных перемычек ядер жесткости. Особенности проектирования пространственных несущих систем на основе каменной кладки, страница 11

2. Собственная жесткость вертикального элемента на изгибное кручение пренебрежительно мала по сравнению с общей жесткостью пространственной системы.

3. Учитывая, что в пространственной несущей системе горизонтальные и вертикальные нагрузки действуют совместно, считается, что растяжение в ядрах жесткости и диафрагмах не возникает, поэтому для сжатых и условно растянутых волокон принимается единый модуль деформации .

4. Собственная центральная система осей ядра жесткости или диафрагмы параллельна осям общей несущей системы.

 Полное перемещение любого междуэтажного перекрытия под действием поперечной силы  от внешних горизонтальных нагрузок, действующей на фасад здания, перпендикулярно оси y складывается из горизонтального смещения Vy и угла поворота вертикальной оси x.

Поворот пространственной системы на угол  осуществляется за счет действия крутящего момента:

,                                                                                      (1)

где  – поперечная сила от горизонтальной нагрузки, приложенной по линии, проведенной через центр фасада.

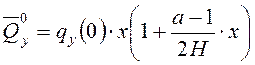 .                                                                        (2)

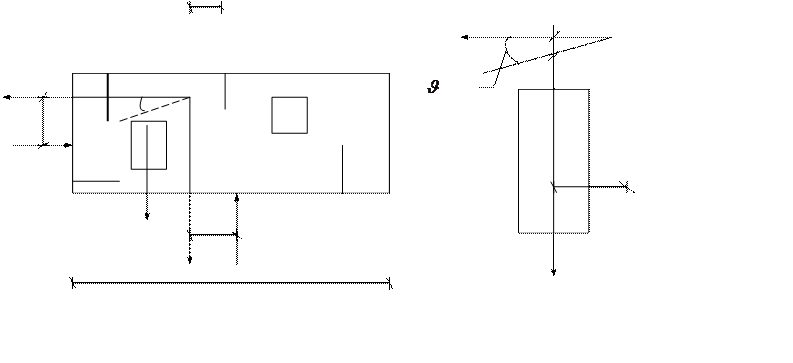
При поступательном смещении перекрытий возникает только изгиб ядер и диафрагм в плоскости YOX. При этом полный момент от горизонтальной нагрузки распределяется пропорционально изгибной жесткости ядер и диафрагм:

                                                        Z                                                                            

                          k                                                                             q

                                                                                                                                                       Z_j

                                         J    y                                                                                

                                             L/2                                       L/2

Рис. 5.1

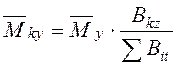               ;                                                                          (3)

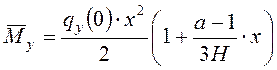               .                                                         (4)

Крутящий момент, воспринимаемый ядро-диафрагмовой системой за счет сопротивления ядер чистому кручению определяется следующим образом

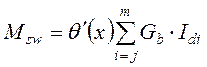               ,                                                                     (5)

где  – первая производная по углу закручивания;  – модуль сдвига бетона ядра жесткости,

.

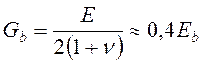Момент, воспринимаемый ядро-диафрагмовой системой из-за изгиба при повороте здания равен:

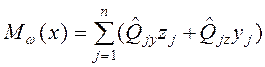,                                                                          (6)

где поперечная сила, воспринимаемая ядрами и диафрагмами при повороте перекрытий;  расстояние от центра жесткости до центра тяжести ядра или диафрагмы;  – горизонтальное перемещение j-го ядра или диафрагмы при повороте (при малых поворотах перекрытий), суммирование производится по всем ядрам и диафрагмам.

Учитывая, что до разрушения пространственной системы она находится в равновесии, то Ms должен быть уравновешен внутренними крутящими моментами

                                .                                                            (7)

Очевидно, что уравнение равновесия (7) можно привести к виду:

  ,                                                                (8)

где .

Дифференцируя уравнение (8) и учитывая, что dMs/dx определяется через интенсивность момента, получим общее уравнение кручения ядро-диафрагмовой системы

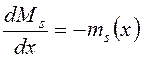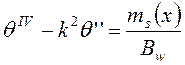  ;                             ,                              (9)

где 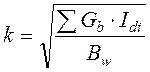 – крутильная характеристика пространственной системы. 

                                               .                                                     (10)

Для уравнения (9) граничные условия имеют вид:

1)  так как элементы системы имеют жесткое сопряжение с фундаментом;

2)  tg угла поворота;

3)  изгибающий момент при повороте;