Особенности обеспечения пространственной жесткости многоэтажных гражданских зданий. Ветровые и сейсмические нагрузки. Расчетные модели диафрагмовых систем. Особенности проектирования надпроёмных перемычек ядер жесткости. Особенности проектирования пространственных несущих систем на основе каменной кладки, страница 12

4)  – изгибающий момент в уровне верха здания при повороте.

Согласно теории дифференциального исчисления решение уравнения (9) с учетом уравнения (10) имеет вид:

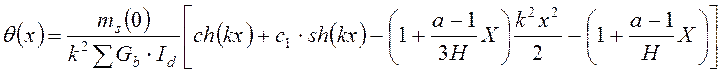,     (11)

где ;      ;     .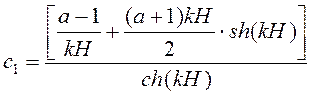

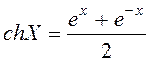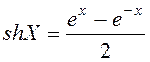Крутящий момент, воспринимаемый одним ядром жесткости за счет его сопротивления чистому кручению равен

.

Изгибающий момент, воспринимаемый ядром или диафрагмой за счет поворота перекрытий определяется интегрированием поперечной силы.

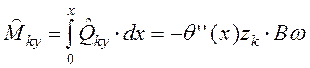 .                                                            (12)

Изгибающий момент, воспринимаемый отдельной диафрагмой или ядром при поступательном смещении определяется из условия (3).

Величина условной горизонтальной нагрузки, приложенной к отдельному ядру или диафрагме, вызванная поворотом перекрытий определяется из условия:

 .                                                                              (13)

Полный изгибающий момент, вызванный внецентренным приложением горизонтальной нагрузки, действующей на отдельную диафрагму или ядро, определяется из условия. 

 .                                                                                       (14)

Полная нагрузка на ядро или диафрагму

,

где 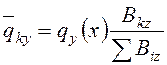  –  горизонтальная нагрузка при поступательном смещении перекрытий.

Прогиб любой вертикальной несущей конструкции в ядро-диафрагмовой системы, вызванный поворотом от горизонтальной нагрузки равен

,                                                                           (15)

а прогиб от поступательного смещения, соответственно

.

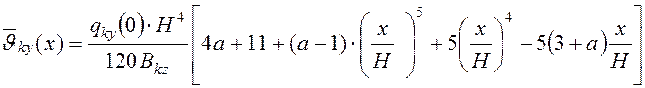Полный прогиб диафрагмы или ядра, вызванный поворотом или смещением от горизонтальной нагрузки определяется в виде суммы:

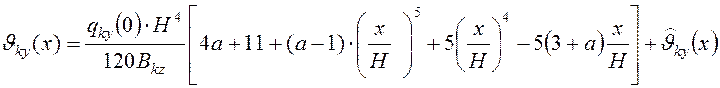 .     (16)

Окончательно для определения полного прогиба ядра или диафрагмы с учетом внецентренного действия вертикальных нагрузок в выражение (16) можно добавить прогибы от соответствующих нагрузок

.

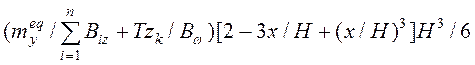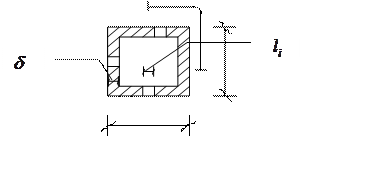
Жесткость на чистое кручение замкнутого контура в плане ядра без проемов с размерами сторон b и t и толщиной стенки  определяется по условия

  .        

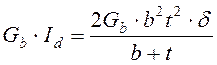Жесткость ядра жесткости на чистое кручение при ослаблении сечения проёмами определяется приближенным способом

,     

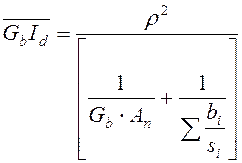где 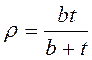;  площадь сечения ядра за вычетом проёмов; -расстояние между центрами тяжести сечений столбов ядра, примыкающих к i-тому проёму;

 (см. рис. 5.2);  – параметр жесткости надпроёмной перемычки, 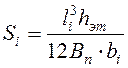;   – размер проёма i-го проема;   – высота этажа;  – изгибная жесткость надпроёмной перемычки;

                                           

                                                t

                              b

Рис. 5.2. Замкнутое в плане ядро жёсткости.

Л Е К Ц И Я    № 6

П Л А Н

6.1. Учет влияния податливости горизонтальных швов в диафрагмовой

       системе и связей сдвига.

6.2. Учет податливости основания на деформирование несущей системы.

6.3. Учет продольного изгиба на деформации и усилия

       диафрагмовой системы.

6.1. Учет влияния податливости горизонтальных швов 

       в диафрагмовой системе и связей сдвига

Во всех расчетных моделях элементы диафрагмовой системы теоретически изначально принимаются монолитными. В системах из сборных конструкций междуэтажные перекрытия делят столбы диафрагм на одноэтажные элементы. Соединение этих элементов осуществляется при помощи растворных или бетонных (мелкозернистых) горизонтальных швов.  

Очевидно, что наличие этих швов снижает общую жесткость диафрагм и увеличивает деформативность всей системы.

Податливость горизонтальных швов принято оценивать приведенным модулем деформации  системы, состоящей из одноэтажной стенки и швов, в пределах одного этажа.

Приравнивая деформации осредненной конструкции и фактической, состоящей из стенки и растворных швов, получим:

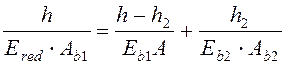        ,                                                              (1)

где высота этажа; площадь  поперечного (горизонтального) сечения стенки диафрагмы; суммарная высота растворных швов в пределах одного этажа; соответственно, модули упругости бетона стенки диафрагмы и шва; , площадь горизонтального сечения растворного шва (преимущественно  и равны).

Из условия (1) определяют по формуле