Математический анализ. Задачи для подготовки к Госэкзаменам

ЗАДАЧА1. Найти дифференциальное уравнение: W(p)=?, построить частотные характеристики, определить переходную характеристику.

   Решение : из  уравнения  материального  баланса  изменение  количества жидкости в баке за время Dt определяется  соотношением между расходами на притоке Q_пр и стоке Q_ст :  или  . Устремив Dt к нулю получим уравнение определяющее состояние  объекта при изменении Q_пр(t) и Q_ст(t)..

Приток Q_пр(t) не зависит от уровня жидкости в баке, а сток Q_ст(t) находится в квадратичной зависимости от перепада давлений , определяющегося величиной уровня жидкости :

 , a - коэффициент расхода.

Если допустить , что отклонение Dh=h-h₀ от исходного  значения уровня h₀ мало , то нелинейную зависимость  можно заменить приближенной линейной . Разлагая  в ряд Тейлора по степеням Dh в окрестности значения h₀  и ограничиваясь двумя первыми членами ряда , получим :

C учетом  и  искомое приближенное уравнение объекта :

Для сокращения записи знак приращения D можно опустить :

,  где a и b – постоянные коэффициенты ;

Линейное уравнение (*) составлено в приращениях ; без  указания исходного режима , в окрестности  которого произведена линеаризация , это уравнение не имеет смысла.

Построим частотные характеристики для объекта , описываемого диф. уравнением :

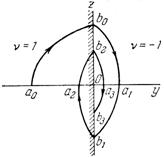
ЗАДАЧА 4. Построить фазовую траекторию в общем виде и  сделать вывод об устойчивости

 

                  

разделим переменные

                    интегрируем при начальных условиях: t=t₀, у=у₀, z=z₀

при у<0:

при у>0:

В начальный момент t=0      Þ                    y₀=a₀, z₀=0

спираль приближается к точке устойчивости (0),

совершая затухающие колебания, т.о. система устойчива.

 

ЗАДАЧА  2. Определить спектр сигнала x(t) = a  t ³ 0.

Решение :  ,

,

        =>