Математический анализ. Задачи для подготовки к Госэкзаменам, страница 5

Вывод :т.к. годограф вектора А(р) начинается при w=0  на вещественной положительной полуоси и не проходит последовательно через 4 квадранта комплексной плоскости в положительном направлении , т.е. против движения часовой стрелки , система не устойчива.

ЗАДАЧА 13. Найти передаточную функцию электрической цепи относительно выходного U_вых и входного  U_вх  напряжений,  построить AUX.

 

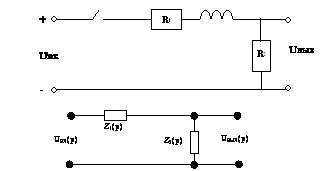Решение :

Запишем выражение для передаточной  функции :

    ,  ,

    => 

где       ,  

,

ЗАДАЧА 11. Определить устойчивость замкнутой системы по  Михайлову методом перемежаемости корней.

Решение : 1. Определяем передаточную функцию замкнутой системы :

2. Характеристическое уравнение системы :

 ,  , ,

X(w)=0   ,   ; w₁=418440,7 ; w₂=9559,3

 ; ;w₁=0 ;w_2,3=±231,35

Re(0)=500 >0   ;  ; Im’(0)= 9,5 >0 ,

т.к. Re(0)=500 >0 и Im’(0)= 9,5 >0 , то замкнутая система устойчива .

ЗАДАЧА 12. Дана импульсно-переходная характеристика

Используя метод Тасина, построить рекуррентный алгоритм моделирования линейного динамического звена.

Решение: ,   , 

Тогда  необходимо minT_i  , maxT_i    :     -  число  периодов

Используя рекуррентный алгоритм :    ,   , проведем дискретизацию : пусть Dt=DQ

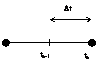
по мат трапеции: соответственно передаточная функция k*(z)

ЗАДАЧА 14. Определить запас устойчивости по модулю и фазе: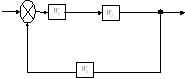

   ;  ;

₁ = 2, k₂ = 10, k₃ = 10;