ЗАДАЧА 18. Определить критическое время запаздывания аналитически
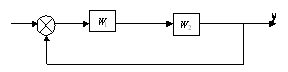
![]() ,
, ![]()
T = 0.05, k = 4
Решение:![]()
 Находим частоту
среза из условия
Находим частоту
среза из условия ![]() ,
, ![]() =>
=> ![]()
![]()
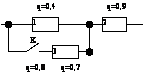 Задача
№ 48
Задача
№ 48P - ?
![]()
ЗАДАЧА 19.
![]()
k=30, Т1=0.025, Т2=0.2. С помощью ЛЧХ определить критическое время запаздывания tкр, ЛАЧХ и ЛФЧХ.
Решение: асимптотическая ЛАЧХ системы:
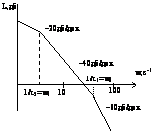 |
j(wc)=–p/2–arctg wc*T1- arctg wc*T2 –wc*tк=–pÞtк=(p/2–arctg wc*T1- arctg wc*T2)/ wc
tк=4.8*10-2c
Составить выражение для определения Кr

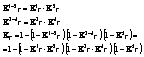
АДАЧА 21. Составить дифференциальное уравнение, получить W(р), построить частотные характеристики.
|
Решение: составим д.у. относительно вх. и вых. сигналов согласно 2 закону Кирхгофа.
Uвх=IR+Uвых (1) выражаем I ч/з Uвых I=c(dUвых/dt)(2), подставляем (2) в (1): Uвх=СR(dUвых/dt)+ Uвых(3) т.к. Т= СR, то выражение (3) примет вид
Т(dUвых/dt)+ Uвых =Uвх(4), запишем его в операторной форме Тр Uвых(р)+ Uвых(р)= Uвх(р)(5)
из выражения (5) находим передаточную ф-ю схемы: W(р)= Uвых/Uвх=1/(Тр+1), если параметры данной схемы записать в операторной форме, т.е. Uвх»Uвх(р), Uвых»Uвых(р),
R»R, хс(р)=1/рс, то исходную схему можно представить, тогда
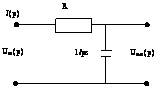
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.