Математический анализ. Задачи для подготовки к Госэкзаменам, страница 4

 ;  

Передаточная функция: Строим логарифмические характеристики:, , =2, 20 lg k = 20 lg 1=0

ЛФЧХ пересекает линию j=-180 ⁰ при  отрицательных значениях асимптотической ЛАЧХ . Следовательно , замкнутая система устойчива .

ЗАДАЧА 9. Передаточная функция разомкнутой системы имеет вид

k=25, Т₁=0.01. Определить условия устойчивости замкнутой  системы и выбрать постоянную времени Т₂ из условия устойчивости.

Решение : Запишем передаточную функцию замкнутой системы :

Характеристический полином замкнутой системы имеет вид :

Составляем матрицу Гурвица :

    ;

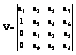D1=a₁=1-T₂ k ,            

ЗАДАЧА 10. САР описывается дифференциальным уравнением

Определить устойчивость.

Решение: 1. Определим передаточную функцию системы: запишем уравнение в операторной форме:

2. Для определения устойчивости запишем матрицу Гурвица :

,,  ,

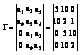т.к. D2 < 0 , то система не устойчива .

3. Критерий Михайлова . Характеристический  полином системы :

Определим вещественную и мнимую части функции D(jw) :

  , 

Вычислим X(w) и Y(w) для ряда значений  частот  w :

w,с-1	0	0,5	1	1,1	1,2	1,3	1,4	1,5	1,45
X(w)	1	1,125	9	13,2	18,9	26,18	35,5	47,13	41
Y(w)	0	4,375	5	4,35	3,36	2,02	0,25	-1,875	-0,74