Колебания атомов в твердом теле. Фононы, их взаимодействие с другими квазичастицами, страница 8

Так как масса всего кристалла весьма велика, то, без нарушения правил сохранения, фотон может передать всему кристаллу импульс без передачи энергии (а значит, и без изменения частоты). Такой процесс называется упругим рассеянием. Частные примеры такого рассеяния это отражение и преломление света на границе раздела сред с разными коэффициентами преломления, Релеевское рассеяние. Раньше мы рассмотрели процесс, когда фотон передают всю свою энергию кристаллу полностью, поглощается. Очевидно, что возможны процессы, когда фотон передаёт кристаллу (либо забирает у него) квант энергии, превращаясь в фотон с другой частотой и импульсом. Такой процесс называют комбинационным рассеянием света или неупругим рассеянием (в англоязычной литературе - Raman scattering, по фамилии одного из первооткрывателей, индийского физика, Нобелевского лауреата Рамана). Справедливости ради стоит отметить, что, этот эффект одновременно с Раманом открыли два российских физика – Г.С.Ландсберг и Л.И.Мандельштам, они же первые дали ему правильную интерпретацию. История открытия и применение данного эффекта красочно описана в обзорной статьё И.Л.Фабелинского в журнале «Успехи физических наук», том 168, №12, стр. 1341, 1998 год. Вообще говоря, фотон может взаимодействовать с любыми квазичастицами в кристалле, мы ограничимся взаимодействием с фононами. Процесс, когда фотон испускает фонон, а сам теряет часть энергии, называется Стоксов процесс. Процесс, когда фотон поглощает фонон, а сам приобретает энергию, называется анти-Стоксов процесс. Схема Стоксова процесса приведена на рисунке 4.10.

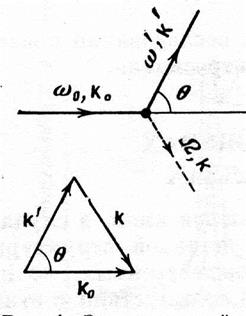
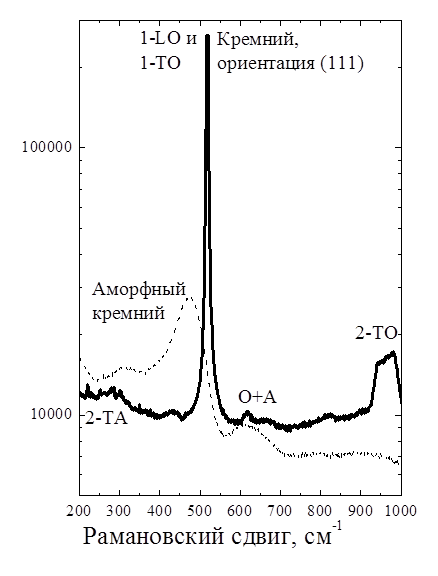
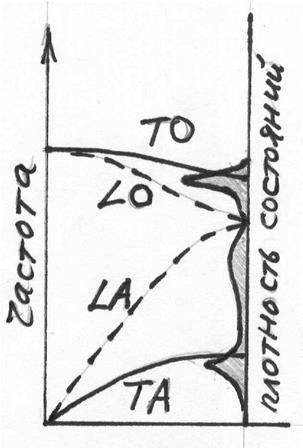
Рис. 4.10. Слева - схема Стоксова процесса комбинационного рассеяния света. Здесь  и k₀ - частота и волновой вектор падающего света,  и k’ - частота и волновой вектор рассеянного света, а  и k – частота и волновой вектор фонона. Треугольник внизу характеризует закон сохранения импульса. Справа – пример одно- и двух-фононого спектра КР света и свёртки плотности колебательных состояний.

В спектре комбинационного рассеяния свет возникают два сателлита с положением , где  - частота падающего света,  - частота рассеянного света, а – частота фонона. Комбинационное рассеяние так и назвали потому, что частота рассеянного фотона представляет собой комбинацию начальной частоты и частоты квазичастицы (с которой фонон взаимодействует). Очевидно, что вероятность анти-Стоксова процесса меньше, чем Стоксова процесса и стремится к нулю при стремлении к нулю температуры кристалла. По соотношению интенсивностей этих процессов можно найти число заполнения фононов и из формулы 4.2 определить температуру кристалла.

Так как должны выполняться правила сохранения энергии и импульса, фотоны взаимодействуют с фононами, импульс которых в ближайшей окрестности центра зоны Бриллюэна (|k₀|@|k’|, 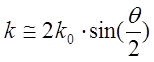 на рисунке 4.10). Рассеяние на акустических фононах называется рассеяние Мандельштама-Бриллюэна. Легко заметить, что фотон при этом теряет либо приобретает очень малый квант энергии. Зная скорость звука и показатель преломления среды, самостоятельно оцените, какую энергию теряет фотон с частотой при рассеянии назад. Гораздо больше комбинаций фононов могут принять участие в рассеянии фотона с участием двух фононов (двухфононные процессы). Так, два поперечных акустических фотона вблизи края зоны Бриллюэна могут иметь суммарный импульс близкий к нулю, и принять участие в рассеянии фотона, дав пик в районе 300 см^-1 (рис. 4.10, центр). Нарушение трансляционной симметрии кристалла (разупорядочение, аморфизация) ведёт к смягчению правил отбора по импульсу, и в рассеянии могут участвовать почти все фононы зоны Бриллюэна. Спектр комбинационного рассеяния в этом случае будет состоять не из нескольких сателлитов, а отображать эффективную плотность колебательных состояний (рисунок 4.10, центр и справа).