Колебания атомов в твердом теле. Фононы, их взаимодействие с другими квазичастицами, страница 7

Решение ищем в виде , тогда 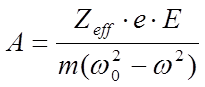, и, можно вычислить дипольный момент ячейки и дипольный момент единицы объёма. Мы не учли затухание колебаний, и поэтому дипольный момент (и, соответственно диэлектрическая проницаемость кристалла 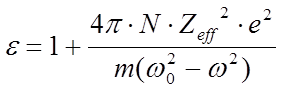, учитывается только вклад ионов, N – концентрация ионов обоих знаков, электроны не учитываем) обращается в бесконечность при . Для ионных кристаллов (и для кристаллов, в которых валентная связь полярна, например полупроводники типа AIIIBV), фотон с частотой поперечного оптического фонона сильно взаимодействует с кристаллической решёткой. Взаимодействие настолько сильное, что приводит к образованию новой квазичастицы – фононного поляритона. Попробуем определить дисперсию фононного поляритона. Для электромагнитной волны  , n – показатель преломления равный . Запишем зависимость показателя преломления от частоты, используя полученную выше формулу. Обратим внимание, что во втором члене числитель, делённый на массу, имеет размерность частоты в квадрате, обозначим её как . Вклад электронов учтем как постоянную добавку к диэлектрической проницаемости. Это оправдано, так как электроны «быстрые» частицы по сравнению с ионами, и поля с характерными для движения ионов частотами для них фактически постоянные, значит, их отклик почти не зависит от частоты в этом диапазоне. Тогда:

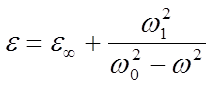               4.3.

И, схематически, можно привести дисперсию смешанного состояния фотон-фонон в ионном кристалле (фононного поляритона) на рисунке 4.9.

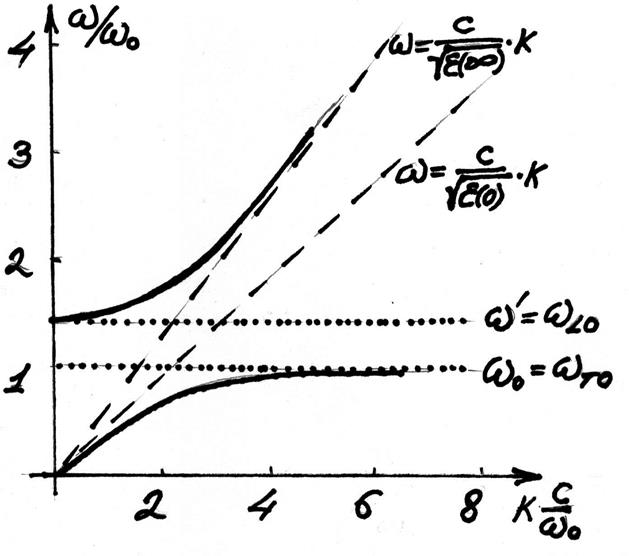
Рис. 4.9. Дисперсия фотона в ионном кристалле. Фононный поляритон.

Видно, что в промежутке от  до некой частоты , электромагнитная волна не может распространяться по кристаллу, диэлектрическая проницаемость отрицательная, а показатель преломления комплексный. В курсе теории твёрдого тела будет показано, что  (частоты фононов приведены в длинноволновом пределе). Дисперсии «чистых, несмешанных» фотона и фононов (если бы не было взаимодействия) показаны штриховыми и точечной линиями соответственно. Дисперсия фононного поляритона показана сплошной линией. Видно, что в ионных кристаллах нет «чистых» фотонов с частотами чуть меньше  и чуть больше, фотон образует смешанное состояние то он рождает фонон (становится фононом), то опять поглощает фонон (становится фотоном). Групповая скорость такой квазичастицы весьма мала, то есть, на этом эффекте можно делать линии задержки оптических сигналов. 

Так как длина волны фотонов, взаимодействующих с фононами составляет от единиц до десятков микрон, методику, исследующую их поглощение и отражение называют инфракрасной спектроскопией (ИК-спектроскопией). ИК-спектроскопия (infrared spectroscopy) позволяет исследовать не только фононы в идеальном кристалле (да и в аморфных телах), но и по интенсивности поглощения на локальных колебаниях примесей, определять их концентрацию. Если дефекты и примеси электрически не активны (не дают уровней в запрещённой зоне), то ИК-спектроскопия пожалуй единственная методика, позволяющая определять их концентрацию. В качестве примера можно привести определение концентрации кислорода, углерода или не активированного бора в кремнии. Помимо правил отбора по энергии и импульсу, в процессе поглощения должны выполняться правила отбора по симметрии, то есть не все фононы, удовлетворяющие правилам отбора по энергии и импульсу, могут быть активны в процессах поглощения. Подробнее об этом смотри в книге 2.1. Весьма упрощённо, можно сказать, что активными будут колебания, которые создают дипольный момент. Возможны также двухфононные процессы, когда поглощаются два фонона одновременно.