Смещение всех атомов в кристалле можно описывать, используя 3N-6 координат смещений каждого атома. Но, используя полученное решение, можно описывать колебания кристалла как сумму колебаний собственных мод. Так как число их огромно (3N-6!), то эти моды образуют квазинепрерывный спектр. Каждая бегущая волна обладает волновым вектором (и, с точностью до постоянной Планка квазиимпульсом) и частотой (энергией). То есть, такую волну можно рассматривать как квазичастицу – фонон. Таким образом, фонон имеет энергию и импульс. Фононом называют как плоскую монохроматическую волну (вообще говоря, занимающую весь кристалл), так и волновой пакет. В последнем случае можно говорить о групповой скорости фонона. Фононы могут участвовать в теплопереносе, вносят свой вклад в теплоёмкость кристалла. Кристаллическая решётка может поглотить либо испустить энергию только определённой порцией (квантом) –фононом. Фононы подчиняются статистики Бозе-Эйнштейна, то есть вероятность того, что, фононное состояние заполнено (число заполнения n) равно:
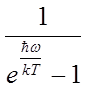 4.2.
4.2.
При высокой
температуре 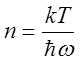 . Следует отметить, что даже при абсолютном
нуле температуры атомы в решётке колеблются (так называемые нулевые колебания),
иначе неопределённость их положения по координате стремилось бы к нулю, нарушая
соотношение неопределённости. Подробнее свойства фонона будут обсуждаться в
курсе теории твёрдого тела (4 курс). Так как синус (формула 4.1) при малых
значениях аргумента можно аппроксимировать линейной функцией, для фононов с
малым волновым вектором фазовая скорость равна групповой. Фононы с частотой от
нескольких герц до десятков килогерц представляют собой звук, поэтому, все
ветки фононов, имеющие нулевую частоту при нулевом волновом векторе называются акустическими
ветвями фононов (попробуйте самостоятельно найти скорость звука из формулы
4.1). Обычно, скорость продольных звуковых колебаний (продольные
акустические фононы – longitudinal
acoustic (LA) phonons) больше чем скорость поперечных звуковых колебаний
(поперечные акустические фононы – transversal acoustic (TA)
phonons). Вспомните существуют ли поперечные звуковые
волны в газах и жидкостях и постарайтесь самостоятельно определить (на
качественном уровне), как связаны скорость «поперечного» и «продольного» звука
и модули Юнга и сдвига кристаллов.
. Следует отметить, что даже при абсолютном
нуле температуры атомы в решётке колеблются (так называемые нулевые колебания),
иначе неопределённость их положения по координате стремилось бы к нулю, нарушая
соотношение неопределённости. Подробнее свойства фонона будут обсуждаться в
курсе теории твёрдого тела (4 курс). Так как синус (формула 4.1) при малых
значениях аргумента можно аппроксимировать линейной функцией, для фононов с
малым волновым вектором фазовая скорость равна групповой. Фононы с частотой от
нескольких герц до десятков килогерц представляют собой звук, поэтому, все
ветки фононов, имеющие нулевую частоту при нулевом волновом векторе называются акустическими
ветвями фононов (попробуйте самостоятельно найти скорость звука из формулы
4.1). Обычно, скорость продольных звуковых колебаний (продольные
акустические фононы – longitudinal
acoustic (LA) phonons) больше чем скорость поперечных звуковых колебаний
(поперечные акустические фононы – transversal acoustic (TA)
phonons). Вспомните существуют ли поперечные звуковые
волны в газах и жидкостях и постарайтесь самостоятельно определить (на
качественном уровне), как связаны скорость «поперечного» и «продольного» звука
и модули Юнга и сдвига кристаллов.
Как мы уже знаем, примитивная ячейка кристалла может содержать более одного атома. В таком случае, число колебательных мод составляет 3L (L - количество атомов в примитивной ячейке). Рассмотрим для примера опять линейную цепочку. Если количество атомов в ячейке 2, период цепочки составляет уже 2a. Если массы атомов (либо жёсткости пружинок) различаются незначительно, то дисперсионное соотношения останется похожим на 4.1, только зона Бриллюэна «свернётся» (рисунок 4.3). Если найти собственные вектора колебаний, то получится, что в нижней ветке, атомы в примитивной ячейке колеблются в фазе, а в верхней – в противофазе. Последняя ветвь называется ветвью оптических фононов. Если массы атомов в примитивной ячейке различны, то, на краю зоны Бриллюэна частоты оптической и акустической ветви продольных колебаний расщеплены (даже в простейшем одномерном случае линейной цепочки). Связано это с тем, что фазы колебаний 2-х атомов в примитивной ячейке на краю зоны Бриллюэна различаются на четверть оборота. Один атом стоит, а второй колеблется. В верхней, оптической ветке колеблется более лёгкий атом, и частота его колебаний выше. Для поперечных мод провал между максимальной частотой акустического фонона и минимальной частотой оптического фонона существует практически всегда. В случае кристалла с решёткой типа алмаза, поперечные оптические (transversal optical (TO)) и продольные оптические (longitudinal optical (LO)) фононы в центре зоны Бриллюэна вырождены.
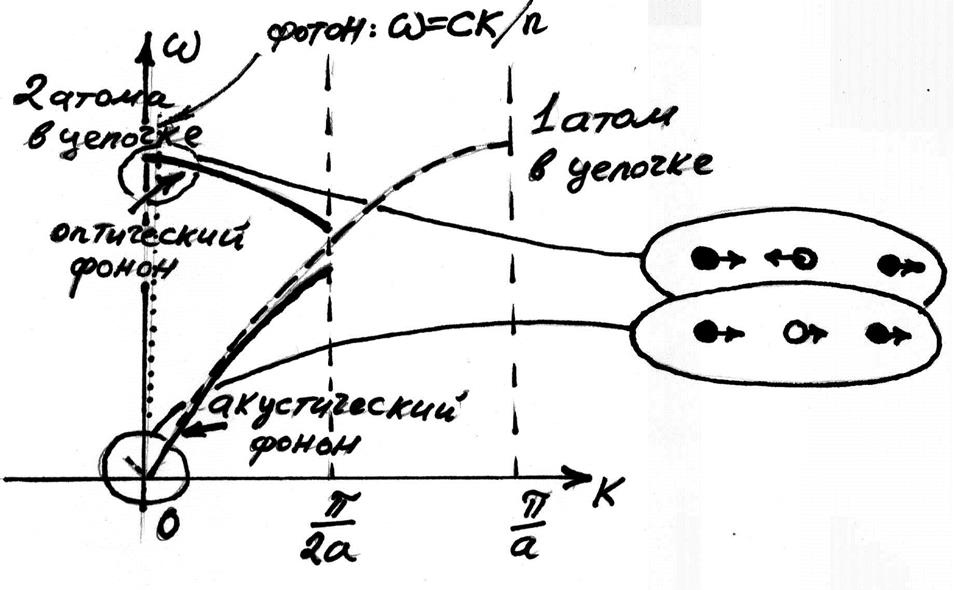
Рис. 4.3. Оптические и акустические фононы в модели линейной цепочки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.