В качестве примера расчётов дисперсии фононов приведены данные для германия (рис. 4.7) и арсенида галлия (рис. 4.8.). Видно неплохое соответствие расчётов с данными эксперимента. Обратите внимание, что частота фонона измеряется в обратных сантиметрах. Делается так в силу исторических причин и удобства. Чтобы получить частоту в герцах, нужно частоту в обратных сантиметрах умножить на скорость света. Энергия фонона равна его частоте, умноженной на постоянную Планка. При этом 1 эВ соответствует примерно 8000 см-1.
На рисунках 4.7 и 4.8 приведены экспериментальные данные по дисперсии фононов, полученные с применением методики рассеяния медленных нейтронов. Для того, чтобы квазичастицы эффективно взаимодействовали между собой, необходимо, чтобы их энергии и импульсы были сравнимы (в силу сохранения энергии и импульса). Нейтроны обладают хорошим свойством – при импульсе в пределах от нуля до края зоны Бриллюэна в кристаллах их энергия близка к диапазону энергий фононов в большинстве кристаллов. Электрон, скажем, более лёгкая частица и при том же импульсе, обладает энергией на несколько порядков больше, чем нейтрон. Нейтроны взаимодействуют с ядрами атомов, отдавая решётке квант энергии – фонон. Задав начальный и определив конечный импульс нейтрона, и определив его начальную и конечную кинетическую энергии можно построить экспериментальные точки, подобные тем, что приведены на рисунках 4.7 и 4.8. Пожалуй, единственный недостаток этого метода (помимо дороговизны) это необходимость исследования довольно массивного объекта (объёмом в несколько кубических сантиметров). К сожалению, некоторые полупроводники удаётся синтезировать только в виде тонких плёнок. Подробнее о методе рассеяния медленных нейтронов смотри в книге 2.2.
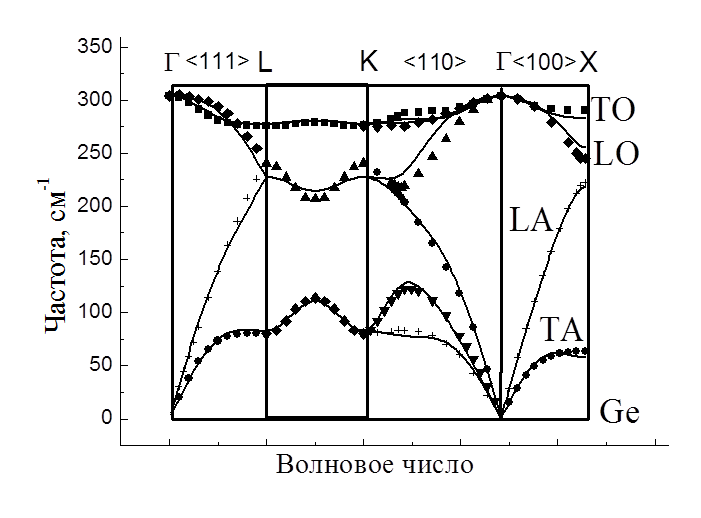
Рис. 4.7. Зависимость частоты фононов в Ge от волнового вектора вдоль высоко-симметричных направлений зоны Бриллюэна. Сплошная линия – расчет с использованием расширенной модели Борна-фон-Кармана. Экспериментальные данные (рассеяние медленных нейтронов) приведены точками.
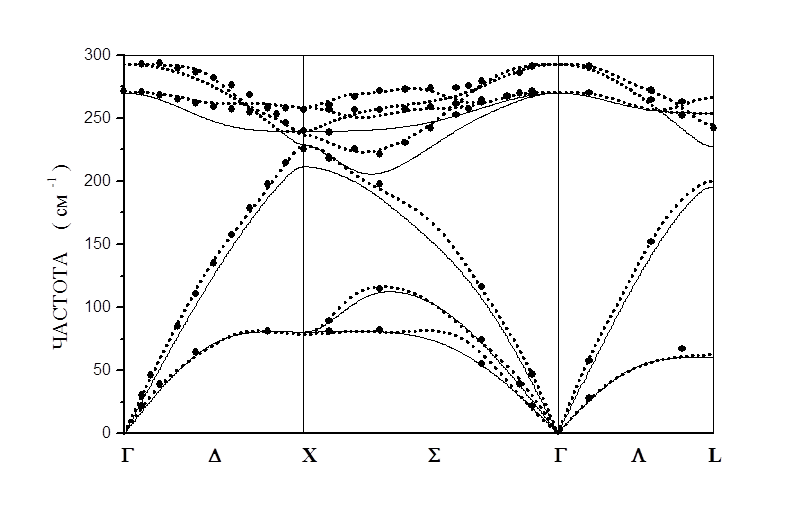
Рис. 4.8. Зависимость частоты фононов в GaAs от волнового вектора вдоль высокосимметричных направлений зоны Бриллюэна. Сплошная линия – расчет с использованием модели заряда на связи, прерывистая линия – расчет с использованием расширенной модели Борна-фон-Кармана. Экспериментальные данные (рассеяние медленных нейтронов) приведены точками.
Для исследования дисперсии фононов используют также неупругое рассеяние электронов и оптические методики, о которых будет рассказано несколько позже.
Как уже обсуждалось в предыдущей лекции, фотоны могут поглощаться, передавая свою энергию и импульс кристаллической решётке, рождая оптический фонон. Известно, что поляризация (направление вектора напряжённости электрического поля) электромагнитной волны поперечна её волновому вектору (по крайней мере, в изотропной среде, в отсутствии свободных зарядов). По этому логично предположить, что фотоны будут поглощаться поперечными оптическими фононами. Рассмотрим, какой отклик в среде вызовет электромагнитная волна, учитывая только фононную составляющую. Так как длина волны фотона много больше размеров примитивной ячейки, поле можно рассматривать как однородное. Рассмотрим ионный кристалл, один ион заряжен положительно, другой отрицательно. Воспользуемся приближением линейной цепочки (рис. 4.2), на каждый ион действует возвращающая сила со стороны пружинок и внешняя сила со стороны электрического поля E.
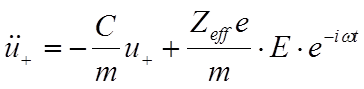
Уравнение для
положительного заряженного иона (суммарная жёсткость возвращающей силы – C, масса ионов – m, Zeff
– эффективный заряд). Пусть, для простоты, массы ионов равны, тогда для
отрицательного иона, уравнение то же, но знак при втором члене отрицательный.
Введём обозначение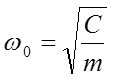 
, тогда:
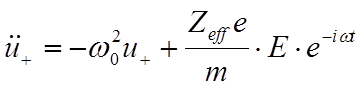
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.