Колебания атомов в твердом теле. Фононы, их взаимодействие с другими квазичастицами, страница 2

Существует также класс молекулярных кристаллов (и кристаллов инертных элементов), молекулы (или атомы) которых связаны между собой слабыми Ван-дер-Ваальсовскими силами. Поэтому, кристаллы с таким типом связей называют Ван-дер-Ваальсовскими кристаллами. Подробнее о природе связей в кристаллах можно прочесть в книге 3.8.

Атомы в кристалле находятся в положении равновесия и равнодействующая всех сил, действующих на каждый атом со стороны всех остальных атомов и электронов, равна нулю. Если разложить зависимость потенциальной энергии от смещения атома из положения равновесия U(r) (рис. 4.1), в ряд Тейлора, то главным членом будет квадратичный. Возвращающая сила пропорциональна смещению, при возмущении из положения равновесия атомы начинают совершать гармонические колебания. Такое приближение называется гармоническим приближением. То, что зависимость потенциальной энергии от смещения атома из положения равновесия отличается от параболы, приводит к эффектам ангармонизма. Прежде всего, это изменение объёма кристалла при увеличении амплитуды колебаний. Так как обычно кривая роста потенциальной энергии более полога при увеличении длины связи, то большинство кристаллов при увеличении температуры (которое приводит к росту амплитуды колебаний) расширяются. Хотя, даже для одного и того же материала, знак коэффициента теплового расширения может меняться несколько раз, в зависимости от температуры.

Даже если мы знаем зависимость U(r) (что, конечно отдельная сложная задача, не решаемая точно в общем случае), рассмотреть динамику кристаллической решётки в гармоническом приближении, решение задачи весьма сложно. Нужно выразить силу, действующую на каждый атом, через смещение всех остальных атомов – составить так называемую силовую матрицу. Количество степеней свободы кристалла равно примерно 3N (три координаты, кристалл содержит N атомов, вообще-то нужно еще учесть движение и вращение кристалла как целого, это на 6 уменьшает количество колебательных степеней свободы). Так как сила, действующая на каждый атом, зависит от положения всех остальных атомов, то, динамическая матрица будет размерностью примерно 3Nx3N. Даже если учесть взаимодействие только с ближайшими соседями (а значит, большинство элементов в матрице равны нулю), найти собственные значения (частоты колебаний) и собственные вектора такой матрицы невозможно.

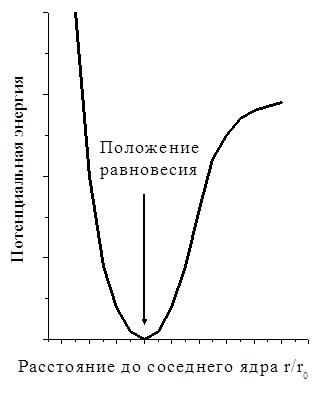
Рис. 4.1. Потенциальная энергия в зависимости от положения атома в кристалле.

Необходимо (как и в случае рассмотрения зонной теории) использовать главное свойство кристалла – трансляционную симметрию. Решение нужно искать в виде бегущих волн, тогда достаточно найти смещение (и частоту колебаний) атомов в примитивной ячейке, а смещение атомов всего кристалла выражается как 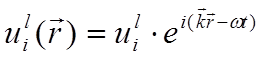. Здесь  - волновой вектор, i координата смещения, l- порядковый номер атома в примитивной ячейке, смещение и частота, вообще говоря, могут зависеть от волнового вектора. Это позволяет снизить размерность динамической матрицы до 3L (L - количество атомов в примитивной ячейке). Число мод также составляет 3L (запомним это!).

Рассмотрим предложенный поход на примере линейной цепочки (задача, знакомая из курса аналитической механики).

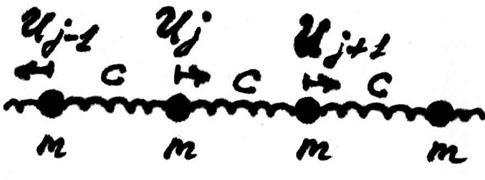
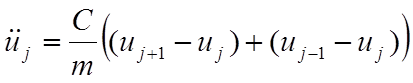
Рис. 4.2. Модель линейной цепочки.

Здесь j – номер атома, жёсткость пружинок – C, масса атомов – m, длина пружинки в положении равновесия - a. Динамическая матрица в одномерном случае сводится к динамическому уравнению.

Если искать решение в виде бегущих волн 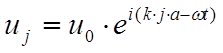, то, получим дисперсионное соотношение (зависимость частоты от волнового числа) для собственных колебаний.

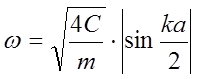      4.1

Колебания с другими частотами в кристалле затухают, то есть не являются собственными. Так как жесткость пружинки в общем случае зависит от направления смещений, то, возможны 3 дисперсионных зависимости (3 моды колебаний). Одна из них продольная мода (вектор смещения вдоль волнового вектора) и 2 поперечных моды (атомы смещаются поперёк волнового вектора). Аналогично, это имеет место и в трёхмерном кристалле.

Как видно из формулы 4.1, зависимость частоты от волнового вектора периодическая. Для описания смещения атомов, волновые вектора по модулю больше чем  не имеют смысла (смотри, например рисунок 3.2). В трёхмерном случае, волновые вектора можно «сложить» в пределы первой зоны Бриллюэна.