Колебания атомов в твердом теле. Фононы, их взаимодействие с другими квазичастицами, страница 5

Подобно задаче нахождения энергетического спектра электронов, задача нахождения спектра колебаний решётки (дисперсии фононов) кристаллов сложна, так как связана с решением квантово-механической задачи многих тел. Условно, методы расчёта дисперсии фононов можно разделить на эмпирические и «ab initio» методы. Последние развиваются в последнее время в связи с распространением суперкомпьютеров, и, по сути, есть попытка в рамках некоторых упрощений решить задачу о нахождении вида потенциальной ямы, в котором находится каждый атом кристалла, из первых принципах. Эмпирические методы обычно просты и построены на ясной физической модели, но требуют знания неких подгоночных параметров, находимых из опыта.

Наиболее простыми моделями является модели силовых констант, одним из представителей которых является модель Борна-фон Кармана (Born-von Karman). Каждой связи приписывается продольная и поперечная жёсткость (силовая константа), рисунок 4.4, в расширенной модели можно учитывать взаимодействие не только с ближайшими соседями, но и с соседями любой координационной сферы. Жёсткости пружинок находятся из соответствия рассчитанной дисперсии и экспериментальных данных. Преимущества данной модели - её простота и неплохое соответствие эксперименту (смотри, к примеру, рисунок 4.7). Основной её недостаток – не ясность физического поведения найденных из подгонки силовых констант. Так, иногда жёсткость пружинок, соединяющих более отдалённые атомы больше, чем жёсткость пружинок, соединяющих более близкие атомы, или жёсткость некоторых пружинок вообще отрицательна. Модель валентных сил Киттинга (valence force Kitting model, в которой потенциальная энергия атома зависит как от длины связи, так и от её угла), также относится к классу моделей силовых констант [3.9 и ссылки в ней].

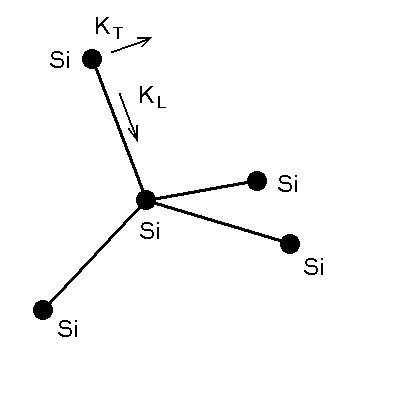
Рис. 4.4. Иллюстрация модели Борна-фон Кармана в применении к кремнию.

В рамках этих моделей кулоновское взаимодействие в случае кристаллов с полярной связью можно учесть, используя модель жёстких ионов (rigid ions). Каждому иону приписывается эффективный (может быть дробным) заряд, и потенциальная энергия при смещении атомов вычисляется в диполь-дипольном приближении. Это, конечно, весьма грубое приближение.

Следующий шаг – учесть то, что ионные остовы окружены электронными облаками. Наиболее просто это сделать в оболочечной модели (shell model), где электронное облако представляется в виде сферической оболочки. Таким образом учитывается дальнодействующее кулоновское взаимодействие положительно заряженных ионов и отрицательно заряженных сфер. Короткодействующие силы представляются в виде пружинок (рис. 4.5), их жёсткость находится из экспериментальных данных. Основным недостатком модели является то, что, например, в случае кристаллов с решёткой типа алмаза, плотность облаков валентных электронов не «размазана» равномерно по сфере, а имеет максимумы в тетраэдрических направлениях (вдоль связей).

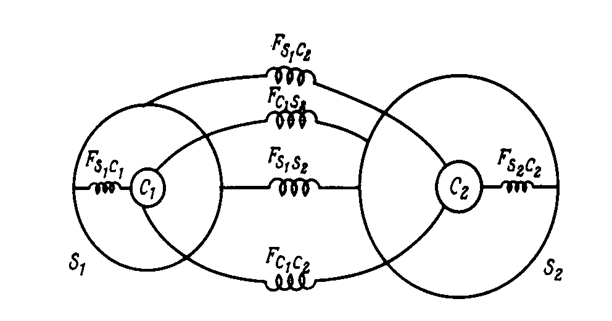
Рис. 4.5. Иллюстрация короткодействующих силовых постоянных в оболочечной модели. Fc₁s₂ обозначает силовую постоянную между остовом 1 и оболочкой 2 и т.д.

Наиболее «продвинутой» из эмпирических моделей является модель заряда на связи (bond-charge model), рисунок 4.6. В ней как раз учитывается, что плотность электронных облаков валентных электронов максимальна в точке, находящейся посередине между атомами (для кристаллов типа алмаза). В кристаллах типа цинковой обманки, заряды на связи смещены в сторону атома с большей электроотрицательностью. Электронное облако заменяется точечным зарядом (и это одно из основных упрощений данной модели) на пружинках. Так как электрон лёгкий, масса его считается нулевой, он мгновенно занимает положение с минимумом энергии, это сокращает количество переменных в динамической матрице (подробности в работе 3.9).

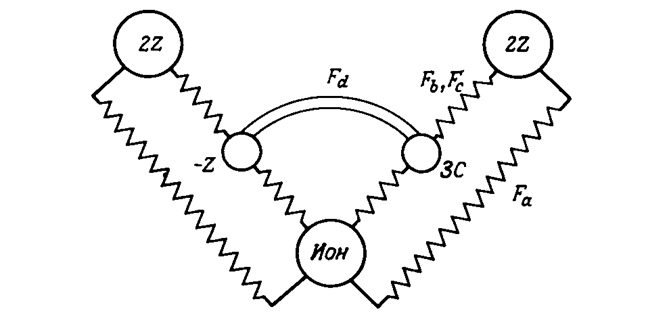
Рис. 4.6. Схематичное изображение модели заряда на связи (ЗС). 2Z– остаточный заряд иона, -Z– заряд на связи. Присутствуют короткодействующие силы между ионами (F_a) и кулоновские силы между ионами и ЗС (F_b). Для стабилизации ЗС на их узлах необходимы короткодействующие силы: ион ЗС (F_c). F_d описывает короткодействующее взаимодействие связь-связь.