Кинетические явления в полупроводниках

Раздел 6. Кинетические явления в полупроводниках.

Лекция 13. Кинетическое уравнение. Подвижность. Проводимость.

Применимость зонной теории в слабых электрических полях. Приближение эффективной массы. Блоховские колебания. Рассеяние электронов и дырок, кинетическое уравнение Больцмана. Малые отклонения от равновесия, время релаксации. Асимметризация функции распределения внешней силой. Дрейфовая скорость. «Греющее поле». Приближение времени релаксации по импульсу. Подвижность. Проводимость.

Вначале дадим определение, что называется кинетическими явлениями в полупроводниках. Явления, обусловленные движением квазичастиц под действием внешних электрических и магнитных полей, градиента температуры и градиента концентрации называются явлениями переноса или кинетическими явлениями. Так как с практической точки зрения наибольший интерес представляет перенос заряда, сузим класс рассматриваемых квазичастиц до электронов и дырок. К явлениям переноса заряда относятся электропроводность, гальваномагнитные, термоэлектрические и термомагнитные эффекты.

Рассмотрим вначале самую простую задачу – движение электрона, находящегося в зоне проводимости под действием однородного постоянного электрического поля. Отметим, что потенциал, в котором находится электрон, теперь уже не периодический, а «наклонный» (рисунок 6.1). Как уже отмечалось в главе 3, даже в периодическом потенциале идеального кристалла, квантовомеханическая задача многих тел нахождения собственных значений и собственных волновых функций электрона не поддаётся решению (даже численному). Требуется сделать упрощения, при этом периодичность потенциала играет ключевую роль. В «наклонном» потенциале уравнение Шредингера не имеет стационарных решений, и, задача, ещё более сложна. Решить её можно, только если внешнее электрическое поле рассматривать как возмущение периодического потенциала. Для этого необходимо условие , здесь E – напряжённость внешнего поля, a – расстояние между атомами. Добавка к соседнему потенциалу должна быть много меньше ширины зон, при этом внешнее поле много меньше внутриатомарных полей. В таком случае можно применять зонную теорию, и, рассматривать задачу движения свободного электрона (с эффективной массой!!!) во внешнем однородном постоянном электрическом поле. Такое (уже встречавшееся нам) приближение называется приближением эффективной массы. Динамическое уравнение тогда можно записать как:

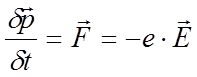
Рассмотрим, что произойдёт при движении электрона с типичной дисперсией (изображённой на рисунке 6.1) в однородном постоянном электрическом поле. Электрон, имея положительную массу и отрицательный заряд движется против поля, набирая импульс и энергию. В некоторой точке дисперсии производная энергии по казиимпульсу становится равной нулю, значит, эффективная масса бесконечна. Далее, эффективная масса становится отрицательной, направление силы остаётся прежним, квазиимпульс растёт, а вот групповая скорость такого электрона начинает уменьшаться. В модели свёрнутых зон Бриллюэна, квазиимпульс определён с точностью до вектора обратной решётки. Достигнув края зоны Бриллюэна, электрон переходит на другой край первой зоны Бриллюэна (мгновенно передав импульс решётке). Теперь импульс его растёт, а энергия уменьшается!!! Он достигает центра зоны Бриллюэна и процесс начинается сначала. Таким, образом, взаимодействие электрона с периодической решёткой приводит к следующему – электрон в постоянном поле совершает колебания. Такие колебания называются Блоховскими. Если задана ширина зоны проводимости вы можете легко оценить амплитуду этих колебаний по координате. Необходимо отметить, что мы пренебрегли вероятностью туннелирования электрона в следующую разрешённую по энергии зону (когда он уже достиг потолка зоны проводимости).

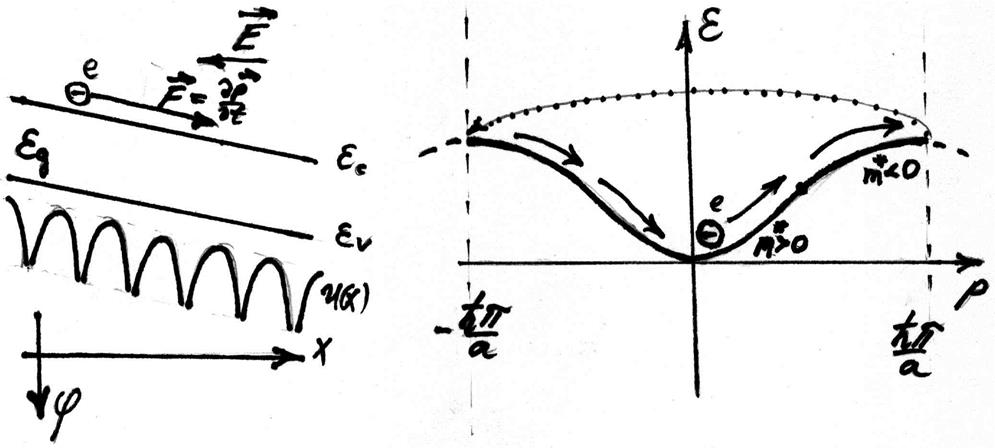
Рис. 6.1. Схематическая иллюстрация возникновения Блоховских осцилляций.

В реальных полупроводниках такое явление никогда не наблюдается. Причиной тому является рассеяние носителей заряда с потерей импульса. Электрон (или дырка) в реальном кристалле при действии внешнего электрического поля не может достичь края зоны Бриллюэна. Внешнее воздействие может изменить функцию распределения частиц по импульсам.

Из предыдущей главы мы знаем, что равновесная функция распределения электронов зависит от их энергии (и, следовательно, от импульса) как:

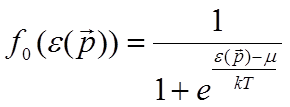
В неравновесной ситуации, функция распределения может зависеть от координаты и от времени  . Рассмотрим элемент фазового объёма . То есть, рассмотрим участок пространства (см. рис. 6.2), а в нём будем следить за электронами с импульсом, принадлежащем промежутку от  до  (и так же по другим проекциям импульса). С учётом спина в данном элементе содержится 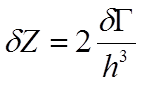 квантовых состояний. Значит, элемент фазового пространства содержит всего электронов.

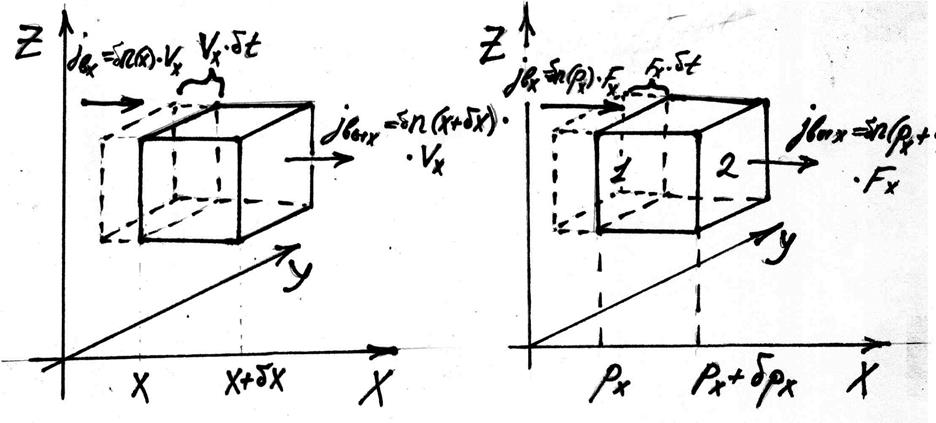
Рис. 6.2. Иллюстрация вывода кинетического уравнения.

Рассмотрим процессы, которые приводят к изменению числа электронов в данном элементе фазового пространства.

1) Это процесс пространственного переноса электронов из близлежащих областей – например их диффузия вследствие градиента концентрации.

2) Действие внешних сил, которые изменяют импульс электронов.

3) Рассеяние электронов на дефектах решётки, на колебаниях решётки, или на других квазичастицах.