Кинетические явления в полупроводниках, страница 3

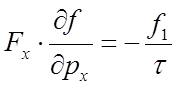
Теперь, в точке , (следовательно, и ) производная функции распределения по проекции импульса  отлична от нуля. Внешнее электрическое поле, приложенное вдоль оси x, асимметризует функцию распределения (рисунок 6.3). Помимо тепловой скорости (не имеющей выделенного направления) у электронов имеется направленная вдоль действия внешней силы средняя дрейфовая скорость. Из предыдущей формулы видно, что для малых отклонений от равновесия она пропорциональна внешней силе. Если дрейфовая скорость много меньше средней тепловой скорости электронов, то, такое поле называют не греющим. При пропускании тока, в этом случае, температура полупроводника меняется незначительно.

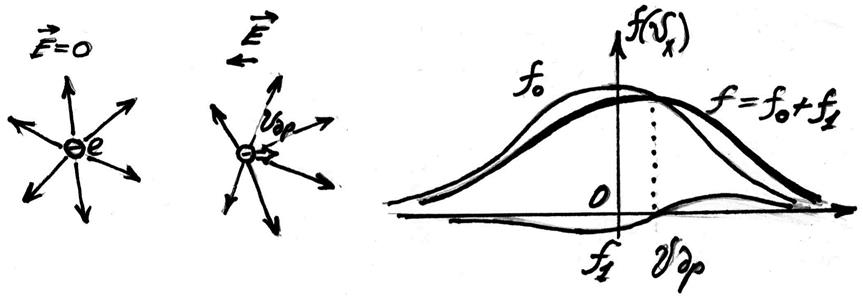
Рис. 6.3. Асимметризация функции распределения внешним полем.

В реальных полупроводниках, как правило, при рассеянии на длинноволновых колебаниях решётки (фононах), либо на неподвижных заряженных примесях, электрон (либо дырка) заметно изменят направление своего движения (квазиимпульс), практически не изменив энергию. Поэтому, ускоряясь под действием внешней силы , за время t достигает некоторой средней скорости V_др, теряет свой импульс (в том числе и добавку к нему, приобретённую за счёт ускорения внешней силой), но, практически не теряет энергии. Если такое приближение справедливо, то, время t называют временем релаксации по импульсу. Так как усреднённая проекция тепловую скорости на любую ось равна нулю, можно весьма грубо рассмотреть движение электрона как ускорение силой в течение времени Dt и мгновенное торможение при столкновении с дефектом, другой квазичастицей, или с фононом [1.4]. Тогда, средняя (дрейфовая) скорость равна: V_др=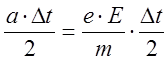. Видно, что чем больше время между столкновениями, тем больше средняя скорость. Как уже обсуждалось, в случае малых отклонений от равновесия, неравновесная добавка к функции распределения (а, следовательно, средняя скорость) пропорциональны внешней силе (а значит и напряжённости электрического поля). Коэффициент пропорциональности между напряжённостью электрического поля и дрейфовой скоростью называется подвижность. Чем подвижнее квазичастицы, тем больший ток они создадут при равной концентрации в том же электрическом поле. Вообще говоря, время релаксации по импульсу зависит от энергии электрона (или дырки) и, правильно считать усреднённую по всем квазичастицам (с учётом функции распределения) подвижность. В самом простом приближении, можно считать время t постоянным для всех квазичастиц, тогда:

V_др=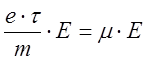, подвижность  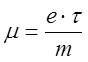                                 (6.7)

Удобная, но внесистемная единица измерения подвижности – см²/В×с. Тогда, можно выразить плотность тока:

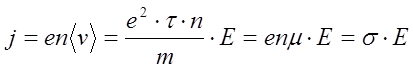                                      (6.8)

Коэффициент s - удельная проводимость полупроводника. Как видно из формулы 6.8, в случае малых отклонений от равновесия (малых полей), в полупроводниках справедлив закон Ома. При наличии нескольких типов носителей заряда, в общий ток суммируется вклад всех типов заряженных подвижных квазичастиц.

Лекция 14. Подвижность носителей заряда в реальных полупроводниках. Сильные электрические поля.

Механизмы рассеяния носителей заряда, температурная зависимость подвижности. Модулированное легирование. Экспериментальные методы измерения удельного сопротивления. «Греющее» поле. Время релаксации по энергии, электронная и фононная температура. Насыщение дрейфовой скорости. Явления в сильном электрическом поле. Эффект Ганна.