Кинетические явления в полупроводниках, страница 4

Оценим подвижность электронов вблизи дна зоны проводимости в типичном полупроводнике, в приближении, что электрон, испытывая столкновение с каждым атомом кристаллической решётки, полностью релаксирует по импульсу. Время свободного пробега (оно же в таком случае время релаксации по импульсу) равно расстоянию между атомами, делённому на среднюю тепловую скорость: 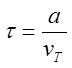. Для невырожденного полупроводника, из соотношения 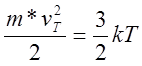, 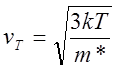. При комнатной температуре, средняя тепловая скорость электронов в арсениде галлия составляет 4×10⁷ см/c. Тогда, для арсенида галлия (межатомное расстояние порядка двух ангстрем), время релаксации по импульсу должно было составлять ½×10^-15 секунды. Масса электрона гамма-долины в арсениде галлия составляет 0.067×9.1×10^-28=0.61×10^-28 грамма, заряд электрона в единицах СГС – 4.8×10^-10, единица напряжённости электрического поля в СГС – 300 В/см. Тогда, исходя из формулы 6.7, подвижность электронов в арсениде галлия должна быть 13 см²/В×с. По экспериментальным данным, в довольно чистом арсениде галлия подвижность электронов составляет 10 000 см²/В×с. Наша оценка оказалась почти на 3 порядка заниженной! Электрон пролетает тысячу атомных расстояний, прежде чем заметно изменит свой импульс!!! Если мы вспомним зонную теорию твёрдого тела, этот кажущийся удивительным результат легко объясним. Электрон в периодическом потенциале – квазичастица. Если потенциал идеально периодический, он не рассеивается на нём (то есть на потенциальных ямах от отдельных атомов). В таком случае, электрон даже в слабом поле может достигнуть края зоны Бриллюэна и испытать Блоховские колебания (смотри начало лекции 13). Далее, постараемся рассмотреть, какие механизмы рассеяния мешают электрону сделать это.

Носители заряда в полупроводниках могут рассеиваться при взаимодействии с:

1.  Фононами;

2.  Ионизованными примесями

3.  Нейтральными дефектами

4.  Поверхностью и границами раздела

5.  Носителями заряда другого типа.

Отметим, что если считать акты рассеяния по различным механизмам независимыми, то полная вероятность рассеяния есть сумма всех вероятностей. То есть, складываются обратные времена релаксации по импульсу - .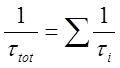

1) В достаточно чистых полупроводниках, даже при криогенных температурах большую роль играет рассеяние электронов (и дырок) на фононах.

Рассмотрим рассеяние на акустических фононах. Количество тепловых фононов (фактор заполнения Бозе-Эйнштейна) растёт с ростом температуры, и, при  пропорционально температуре. Вследствие закона сохранения квазиимпульса, квазиимпульс фонона, с которым может взаимодействовать электрон не может превышать двух квазиимпульсов электрона. Так как большинство электронов имеют энергию от нуля до , их импульс ограничен величиной , значит, с ростом температуры, растёт и количество фононных мод, способных принять участие в процессе рассеяния. Количество акустических мод, ограниченных неким квазиимпульсом p, растёт как p³. Поэтому, вероятность рассеяния электронов на акустических фононах сильно растёт с ростом температуры степенным образом - 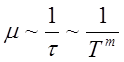. Более точные оценки приведены в книгах 2.1 и 2.3. Принимая во внимание только этот механизм рассеяния, получаем, что при низких температурах, подвижность растёт неограниченно. Как уже отмечалось, энергия электрона при рассеянии на акустическом фононе практически не меняется. Заметно изменить свою энергию электрон может только испустив оптический фонон. Об этих процессах поговорим позднее.

2) Электрон, как заряженная частица взаимодействует с ионизованными примесями по кулоновскому механизму. Из курса механики и электродинамики вы помните, что в кулоновском поле налетающая частица изменяет свою поперечную составляющую импульса. Это изменение тем больше, чем меньше прицельный параметр и скорость частицы. Тепловая скорость электронов пропорциональна , а вероятность того, что электрон пролетит рядом с ионизованной примесью, растёт с ростом концентрации примесей. Поэтому, вероятность рассеяния растёт с ростом концентрации примесей и с понижением температуры. Поэтому, при низких температурах доминирует этот механизм рассеяния. Если концентрация свободных электронов велика, необходимо учесть Дебаевское экранирование потенциала заряженной примеси. Тогда, с ростом концентрации электронов их подвижность будет расти.