Кинетические явления в полупроводниках, страница 8

Определив среднюю (дрейфовую) скорость носителей заряда в скрещенных электрическом и магнитном полях, можно определить холловскую подвижность (которая, будет являться теперь тензором). В случае малых магнитных полей, это почти диагональный тензор. Строго говоря, подвижность, экспериментально определяемая из измерения постоянной Холла отличается от подвижности, определяемой по формуле 6.7. Только если время релаксации не зависит от энергии (и скорости) частицы, холловская подвижность совпадёт с подвижностью определяемой по формуле 6.7.

Определим, какие поля будут малыми – то есть при каких полях угол q будет мал. Следуя формуле 6.10: 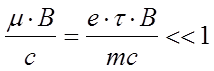. Величина  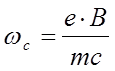известна как циклотронная частота – с такой частотой вращаются электроны в магнитном поле (если отсутствует электрическое поле). Значит, магнитное поле можно считать малым, если .

В отсутствии электрического поля в сильных магнитных полях , носители заряда вращаются по циклотронным орбитам с Ларморовским радиусом 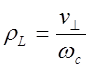, где  - перпендикулярная к магнитному полю компонента скорости. Значит, движение заряженных частиц ограничено по двум координатам, они «заквантованы» в магнитном поле. Расстояние между уровнями их квантования в магнитном поле (уровнями Ландау) составляет . Энергетический спектр электронов и дырок в магнитном поле будет отличаться от спектра свободных электронов и дырок. Он будет схож с энергетическим спектром квантовых проволок (будет обсуждаться в главе, посвящённой полупроводниковым структурам пониженной размерности). Особенно ярко эффекты квантования будут проявляться, если . При пересечении уровня Ферми уровня Ландау, заселённость этого уровня становится равной ½, свойства электронного газа определяются заселённостью уровней Ландау. Положение уровней Ландау зависит от магнитного поля, и, свойства электронного газа зависят от магнитного поля по некоторому (периодическому) закону. При возбуждении электромагнитной волной электрон может перейти на более высокий уровень Ландау, при этом, когда частота возбуждения совпадает с циклотронной частотой, наблюдается резонансное поглощение, называемое циклотронным резонансом. Так как циклотронная частота зависит от эффективной массы, её можно определить из циклотронного резонанса. Меняя направление магнитного поля, можно исследовать анизотропию эффективной массы.

Рассмотрим теперь влияние электрического поля. Из курса электродинамики известно, что свободный заряд в скрещенных электрическом и магнитном полях будет совершать периодическое движение по циклоиде, дрейфуя со скоростью 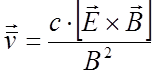. Таким образом, если бы не было рассеяния носителей заряда, действие магнитного поля привело бы к тому, что потенциал в образце (рис. 6.9) перераспределился бы таким образом, что падение напряжения между контактами 3-4 не было, а напряжение между контактами 3-5 и 4-6 определялось бы дрейфовой скоростью, зависящей от тока I и концентрации носителей заряда. Нечто похожее обнаружили и первооткрыватели квантового эффекта Холла фон Клитцинг с коллегами. Существенно важно, что носители заряда были «заквантованы» ещё и в направлении параллельном магнитному полю. С учётом спина, на каждом уровне Ландау может находиться два электрона. Таким образом, если уровень Ферми выше n уровней Ландау, то фактор заполнения равен 2n. При целочисленном (чётном) факторе заполнения они увидели падение до нуля напряжения между контактами 3-4, Холловское напряжение при этом выходило на плато и не менялось, пока не изменялся фактор заполнения. При этом соотношение Холловского напряжения к току было кратно кванту сопротивления  (25813 Ом). Такой режим называется целочисленным квантовым эффектом Холла. За открытие этого эффекта фон Клитцингу была присуждена Нобелевская премия по физике.

Почему в режиме квантового эффекта Холла носители заряда не испытывают рассеяния требует сложного теоретического рассмотрения, и будет обсуждаться в спецкурсах, читаемых для магистрантов.

Лекция 16.