4) Рекомбинация электронов (с дырками) или их генерация, их захват на локальные уровни («ловушки») или их выброс с ловушек.
1- Чтобы
посчитать изменение количества электронов в элементе фазового объёма за некий
промежуток времени из-за действия первого механизма, нужно просуммировать их
поток через каждую грань кубика ![]() . На рисунке 6.2
проиллюстрировано вычисление потока через грани, перпендикулярные оси X. Нужно вычислить дивергенцию потока
. На рисунке 6.2
проиллюстрировано вычисление потока через грани, перпендикулярные оси X. Нужно вычислить дивергенцию потока ![]() .
Но, учитывая, что импульс (а, следовательно, и скорость) рассматриваемых
электронов лежит в узком промежутке фазового пространства, то, скорость можно
считать не зависящей от координаты. Тогда, вследствие первого механизма:
.
Но, учитывая, что импульс (а, следовательно, и скорость) рассматриваемых
электронов лежит в узком промежутке фазового пространства, то, скорость можно
считать не зависящей от координаты. Тогда, вследствие первого механизма:
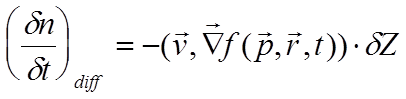 (6.1)
(6.1)
градиент здесь обычный, по координате.
2- Рассмотрим,
сколько частиц покидает элемент фазового объёма или проникает в него за единицу
времени вследствие действия внешних сил. Сила вынуждает электроны менять
квазиимпульс 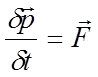 . Предположим, сила ускоряет
электроны, тогда, за малый промежуток времени
. Предположим, сила ускоряет
электроны, тогда, за малый промежуток времени ![]() ,
электроны, имевшие импульс в промежутке от
,
электроны, имевшие импульс в промежутке от ![]() до
до ![]() перейдут грань 1 кубика (рисунок 6.2
справа). При этом электроны, имевшие импульс в промежутке от
перейдут грань 1 кубика (рисунок 6.2
справа). При этом электроны, имевшие импульс в промежутке от ![]() до
до ![]() покинут
кубик через грань 2. Итого:
покинут
кубик через грань 2. Итого:
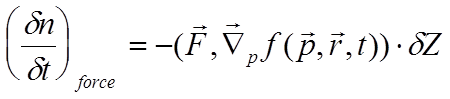 (6.2)
(6.2)
градиент берётся в импульсном пространстве.
3- Рассмотрим
столкновительный механизм. Пусть электрон имел некий импульс ![]() , и, в результате столкновения его импульс
стал равным
, и, в результате столкновения его импульс
стал равным ![]() , принадлежащий рассматриваемому нами
элементу фазового объёма. Процесс столкновения будем рассматривать как
практически мгновенный, локальный процесс, координата электрона не изменилась.
Вероятность такого перехода пропорциональна количеству электронов с импульсом
, принадлежащий рассматриваемому нами
элементу фазового объёма. Процесс столкновения будем рассматривать как
практически мгновенный, локальный процесс, координата электрона не изменилась.
Вероятность такого перехода пропорциональна количеству электронов с импульсом ![]() , количеству свободных мест для электронов
в рассматриваемом элементе, и, собственно вероятности перехода. Заметим, что
вероятность перехода может зависеть от внешнего воздействия, но, если внешнее
электрическое поля много меньше внутриатомарных полей, этой зависимостью можно
пренебречь. Тогда, приход таких электронов в данный элемент равен:
, количеству свободных мест для электронов
в рассматриваемом элементе, и, собственно вероятности перехода. Заметим, что
вероятность перехода может зависеть от внешнего воздействия, но, если внешнее
электрическое поля много меньше внутриатомарных полей, этой зависимостью можно
пренебречь. Тогда, приход таких электронов в данный элемент равен:
![]()
Уход электронов из элемента фазового объёма равен:
![]()
Чтобы найти
полный баланс, нужно сложить эти выражения, и проинтегрировать по ![]() .
.
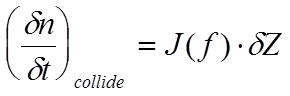 (6.3)
(6.3)
где 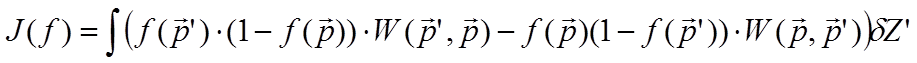 - интеграл столкновений.
- интеграл столкновений.
Заметим, что в случае равновесного распределения, интеграл столкновений равен нулю (при любых пределах), и, следовательно:
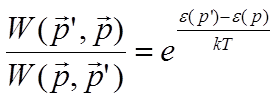
4- Допустим, полупроводник освещается фотонами с энергией, достаточной для генерации электрон-дырочных пар. Тогда, в единицу времени, в полупроводнике рождается некоторое количество электронов с определённым импульсом. Пусть этот импульс попадает в выбранный нами элемент фазового объёма. Тогда:
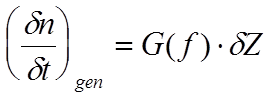 (6.4)
(6.4)
Рассмотрим ситуацию, когда генерационный член равен нулю. Тогда, полное изменение функции распределения равно:
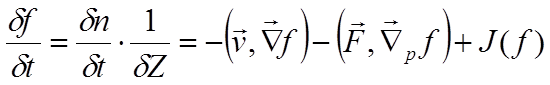 (6.5)
(6.5)
Это выражение называют кинетическим уравнением Больцмана, и, вообще говоря, его необходимо решать для всех типов свободных зарядов.
Рассмотрим
случай, когда внешнее воздействие лишь слегка меняет равновесную функцию
распределения. Функцию распределения представим в виде суммы равновесной и
малой добавки: ![]() , где
, где ![]() . Тогда,
выражение 6.5 можно несколько упростить. Вследствие принципа детального
равновесия интеграл столкновений от равновесной функции равен нулю, тогда:
. Тогда,
выражение 6.5 можно несколько упростить. Вследствие принципа детального
равновесия интеграл столкновений от равновесной функции равен нулю, тогда:
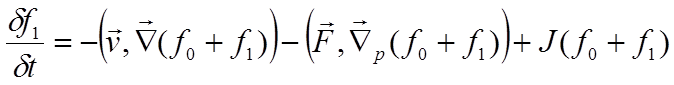 (6.6)
(6.6)
Рассмотрим
случай однородного полупроводника, тогда пространственный градиент функции
распределения равен нулю. Рассмотрим, что будет, если в момент времени t=0 выключить внешнее воздействие. Разложим интеграл
столкновений по малости ![]() . С учётом того, что от
. С учётом того, что от ![]() он равен нулю, а, ассимптотически по
времени функция распределения должна стремиться к равновесной:
он равен нулю, а, ассимптотически по
времени функция распределения должна стремиться к равновесной:
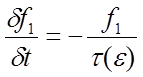
Коэффициент t имеет размерность времени, может зависеть от энергии электронов, и называется временем релаксации.
Рассмотрим
функцию распределения электронов по проекции скорости ![]() .
В условиях равновесия в невырожденном полупроводнике эта функция соответствует
распределению Максвелла
.
В условиях равновесия в невырожденном полупроводнике эта функция соответствует
распределению Максвелла 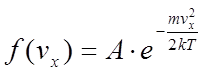 .
Средняя проекция скорости равна нулю. Приложим вдоль оси x
электрическое поле E. Спустя некоторое время
установится неравновесная функция распределения. В условиях динамического
равновесия её производная по времени равна нулю. Рассмотрим также случай
однородного полупроводника. Тогда, из уравнения 6.6, с учётом малости
«неравновесной» добавки:
.
Средняя проекция скорости равна нулю. Приложим вдоль оси x
электрическое поле E. Спустя некоторое время
установится неравновесная функция распределения. В условиях динамического
равновесия её производная по времени равна нулю. Рассмотрим также случай
однородного полупроводника. Тогда, из уравнения 6.6, с учётом малости
«неравновесной» добавки:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.