Кинетические явления в полупроводниках, страница 10

Эффект Пельте. Эффект Пельте, в общем, противоположен эффекту термо-ЭДС. При пропускании тока, электроны переносят через образец не только заряд, но и кинетическую и потенциальную энергию. Если пропускать ток, через образец, рассмотренный в предыдущем примере, в таком направлении, что электроны движутся от более холодного образца к более горячему, они переносят энергию от холодного конца к горячему. То есть, такой ток охлаждает более холодный контакт. Эффект Пельте используется в холодильниках Пельте.

Из термомагнитных явлений рассмотрим поперечный эффект Нернста-Эттингсгаузена. Рассмотрим полупроводник, в котором есть градиент температуры, помещённый в магнитное поле. Пусть магнитное поле перпендикулярно направлению градиента температуры. Замкнём холодный и горячий контакты полупроводника, и в нём потечёт ток, индуцированный термо-ЭДС. В этом случае в образце возникнет электрическое поле в направлении перпендикулярном и магнитному полю, и градиенту температуры. Эффект Нернста-Эттингхаузена возникает по той же причине, что и эффект Холла. Только направленное движение заряженных частиц вызвано теперь не внешним полем а диффузионными потоками. И электроны и дырки движутся от горячего контакта к холодному, отклоняясь в магнитном поле. Стоит заметить, что отклоняются они (в силу разного знака заряда) в разные стороны, но поле создают (опять же в силу разного знака заряда) одного направления. Поэтому, по направлению электрического поля в данном эффекте нельзя определить знак носителей заряда.

При выводе кинетического уравнения Больцмана, мы, фактически, учли все виды токов, протекающих через полупроводник – полевой (из за внешней силы), диффузионный и генерационный. Рассмотрим для простоты полупроводник, в котором неосновными носителями заряда можно пренебречь, ток определяется основными носителями. Взаимодействием основных носителей заряда с неосновными (генерацией и рекомбинацией) также пренебрежём. Рассмотрим одномерный случай, полупроводник пусть будет n типа. Тогда плотность тока равна:

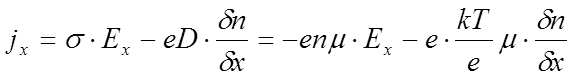                       (6.15)

Если измерять потенциальную энергию электронов в электрон-вольтах, то:

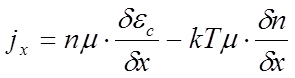
Выразим градиент концентрации через положение уровня Ферми (в общем случае квазиуровня Ферми). Напомним, что в невырожденном полупроводнике .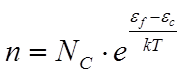

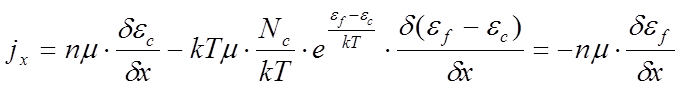            (6.16)

Таким образом, ток через полупроводник пропорционален концентрации свободных носителей, подвижности, и градиенту уровня Ферми. Если приложить напряжение к неоднородно легированному полупроводнику, в установившемся режиме через него потечёт постоянный однородный ток. Если заряды нигде не накапливаются, дивергенция плотности тока равна нулю, и, в одномерном случае плотность тока не зависит от координаты. Значит напряжение падает в основном на участках с малой концентрацией носителей (с большим удельным сопротивлением).

То, что плотность тока пропорциональна градиенту уровня Ферми является общей зависимостью, можно показать что это справедливо и для вырожденных полупроводников.

Задание.

1) Электрон гамма-долины в арсениде галлия с энергией kT испустил продольный акустический фонон, почти упруго отразившись назад. Оценить, какую часть энергии потерял электрон в данном процессе. Масса электрона 0.067m_e, скорость «продольного» звука в арсениде галлия примерно 2.7·10⁵ см/с.

2) Определить концентрацию электронов и дырок при комнатной температуре в кремнии марки КЭФ-4.5. Кремний с электронным типом проводимости, легирован фосфором, удельное сопротивление при комнатной температуре составляет 4.5 Ом·см. Подвижность электронов считать 1300 см²/В×с.

3) Полупроводник легирован неоднородно, тип его проводимости у левого контакта p-типа, у правого – n-типа. Качественно нарисовать зонную диаграмму полупроводника, при приложении к нему напряжения U.