Кинетические явления в полупроводниках, страница 6

Электрическое поле, которое заметно изменяет функцию распределения частиц, называется сильным полем. Поле, в котором дрейфовая скорость уже становится сравнимой с тепловыми скоростями, называется греющим полем. Оценим величину этого поля для арсенида галлия. Подвижность электронов и дырок в основных полупроводниках при комнатной температуре и при температуре кипения жидкого азота приведены в таблице 6.1.

Таблица 6.1. Подвижность электронов и дырок в основных полупроводниках.

Как мы уже оценили, при комнатной температуре, средняя тепловая скорость электронов в арсениде галлия составляет 4×10⁷ см/c. Электрон достигнет такой дрейфовой скорости в поле 4×10³ В/c. В полях такого масштаба электрон может приобретать добавочную энергию, сравнимую с тепловой. Если такое поле приложить в течении короткого импульса, в полупроводнике сгенерируются «горячие» электроны и дырки. «Горячие» носители заряда можно создать также оптическим возбуждением либо инжекцией извне. В зависимости от типа полупроводника, «горячие» носители заряда могут передавать свою энергию либо решётке (испуская оптические фононы, с энергией 30-40 мэВ), либо другим электронам. Среднее время, в течение которого электрон испускает оптический фонон в полярном полупроводнике, составляет около 1 пикосекунды. «Горячему» электрону необходимо испустить несколько оптических фононов (сразу, или последовательно), чтобы потерять избыточную энергию. Таким образом, время релаксации электрона по энергии в полярном полупроводнике составляет несколько пикосекунд. Если в полупроводнике достаточно много свободных электронов, то, время электрон-электронного взаимодействия мало, и, возможна ситуация, когда «горячий» электрон передаёт избыточную энергию другим электронам не успевая нагреть решётку. Электрон «термализуется», при этом некоторое время возможна неравновесная ситуация, когда электронная температура выше фононной температуры.

Как уже было отмечено, в сильном электрическом поле электрон способен набрать энергию больше чем тепловая, при этом он способен практически мгновенно (время 1 пикосекунда гораздо меньше времени релаксации по импульсу) передать энергию (и импульс!) оптическим фононам. Оценим, за какое время электрон наберёт избыточную энергию : 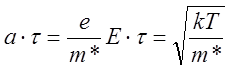. Тогда время релаксации равно 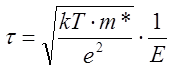. Получается, что время релаксации (и подвижность!) обратно пропорционально напряжённости поля, а дрейфовая скорость уже не растёт. Наступает насыщение дрейфовой скорости.

В некоторых полупроводниках в сильных полях возможен эффект, когда электрон, ускоряясь полем, приобретает энергию, достаточную для того, чтобы перейти в другую долину. Если эффективная масса в этой долине больше, плотность состояний в ней больше (больше мест для электронов), а подвижность меньше. Тогда, с ростом напряжённости поля возможно даже снижение дрейфовой скорости, усреднённой по всем долинам (рис. 6.7). В некоторой области напряжений, такой полупроводник обладает отрицательным дифференциальным сопротивлением – при увеличении подаваемого на него напряжения ток через него уменьшается.

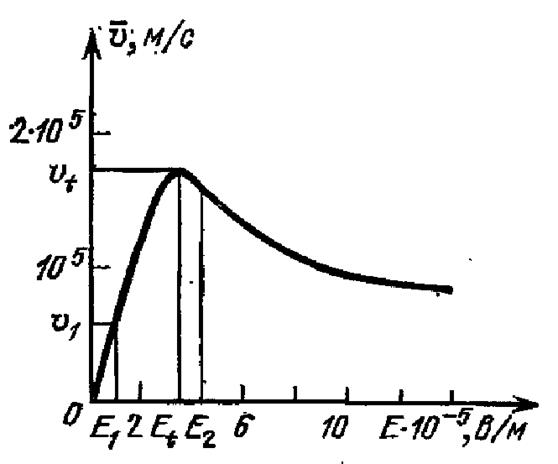
Рис. 6.7. Зависимость дрейфовой скорости электронов от напряжённости электрического поля для арсенида галлия.

На этом эффекте основан эффект Ганна. Американский физик Ганн обнаружил, что при подаче на арсенид галлия постоянного напряжения, проходящий через него ток пульсировал. Этот эффект имеет довольно простое объяснение. Если в образце, среднее поле в котором чуть меньше E_t, возникла флуктуация повышенного сопротивления, в этом, так называемом «домене», напряжённость электрического поля больше, чем в среднем по образцу, и может превысить E_t. Тогда, домен не рассасывается, а увеличивается. Более быстрые электроны догоняют его, заряжая левую его границу отрицательно, а более быстрые электроны справа убегают от него, заряжая его правую границу положительно (рис. 6.8). Домен может расти до тех пор, пока дрейфовая скорость опять не начнёт расти с напряжённостью поля (эта область полей не показана на рисунке 6.7). Когда такой домен достигает контакта, возникает импульс тока. Зная длину образца и дрейфовую скорость домена, можно определить частоту импульсов.