Кинетические явления в полупроводниках, страница 9

Диффузия. Соотношение Эйнштейна. Неравновесные носители заряда. Время жизни неравновесных носителей заряда. Амбиполярная диффузия. Термоэлектрические и термомагнитные явления. Связь плотности тока и градиента квазиуровня Ферми в полупроводниках.

Как уже отмечалось в лекции 13, упорядоченное движение заряженных частиц (ток) может вызвать не только электрическое поле, но и их диффузия (в случае, если есть градиент концентрации по координате). Рассмотрим носители заряда одного типа, например, электроны. Будем считать, что концентрация меняется только вдоль координаты x. С учётом отрицательного заряда электрона, плотность «диффузионного» тока равна:

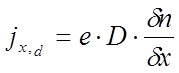                             (6.13)

Из молекулярной физики известна связь между коэффициентом диффузии и длиной свободного пробега: . Длина свободного пробега равна произведению тепловой скорости на время релаксации по импульсу, тогда: 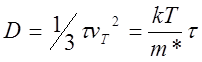. Отсюда, если вспомнить определение подвижности, получается соотношение, называемое соотношение Эйнштейна, определяющее связь между коэффициентом диффузии и подвижностью:

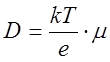                                         (6.14)

В полупроводниках (в отличие от металлов) под влиянием внешних факторов (освещения или инжекции внешним полем) концентрация электронов и дырок может изменяться на много порядков. Например поток фотонов с частотой выше некторого порога может, практически не нагрев образец заметно увеличить в нём концентрацию электронов и дырок. Избыточные носители зарядов, рождённые под воздействием внешних факторов, называются неравновесными носителями зарядов. Мы уже обсуждали это, когда ввели понятие квазиуровня Ферми. Неравновесные носители зарядов рекомбинируют (по различным механизмам), и, при малых отклонениях от равновесия, при выключении внешнего воздействия, функция распределения стремиться к равновесной функции по экспоненциальному закону. Связано это с тем, что неравновесные носители заряда имеют конечное время жизни. Неравновесные носители заряда можно зарегистрировать, например, по изменению электропроводности полупроводника. Можно измерить групповую скорость пакета неравновесных носителей заряда, прикладывая короткие импульсы к части образца называемой эмиттером, и, измеряя (в тянущем электрическом поле) падение напряжения на нагрузочном сопротивлении в цепи коллектора (смотри стр. 265, 2.3).

Осветим часть полупроводника фотонами с энергией, достаточной для генерации электрон-дырочных пар. В неосвещённой части полупроводника Электронов и дырок меньше, чем в освещённой части, поэтому, неравновесные носители заряда будут диффундировать вглубь затемнённой части образца. Подвижность более легких электронов (например, в кремнии, германии и арсениде галлия) больше, чем подвижность дырок. Поэтому, они, казалось бы, должны быстрее диффундировать. Но, необходимо учесть, что и дырки и электроны являются заряженными частицами. Убежавшие электроны создают поле, которое ускоряет оставшиеся дырки и замедляет электроны – поле амбиполярной диффузии. Величину коэффициента амбиполярной диффузии можно найти (смотри, например § 8, главы VII, 2.3).

Закончим главу, посвящённую изучению кинетических явлений в полупроводниках, качественным рассмотрением термоэлектрических и термомагнитных явлений.

Термо-ЭДС. Рассмотрим полупроводник n типа, концы которого находятся при разных температурах. Пусть, для определённости, температура левого торца T₁ меньше температуры правого торца T₂. Электроны, начнут диффундировать от горячего края полупроводника к холодному. Если цепь разомкнута (сопротивление вольтметра для измерения ЭДС на много порядков больше сопротивления образца), тока нет. Значит, в установившемся равновесии, в полупроводнике установится электрическое поле, потенциал которого препятствует движению электронов с горячего торца к холодному. Попробуйте самостоятельно качественно изобразить зонную диаграмму и уровень Ферми в данном случае. Таким образом, с помощью термозонда, по знаку напряжения можно установить тип проводимости полупроводника. Явление термо-ЭДС имеет место и в металлах (эффект Зеебека), но в полупроводниках, этот эффект заметно сильнее.