Кинетические явления в полупроводниках, страница 7

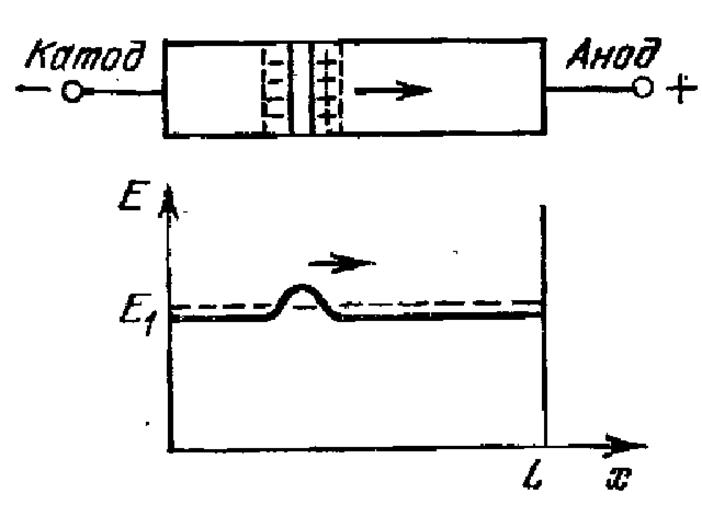
Рис. 6.8. Распределение поля и заряда внутри домена, поясняющее эффект Ганна.

Эффект Ганна применяется в диодах Ганна, использующихся для генерации СВЧ колебаний.

Лекция 15. Полупроводники в магнитном поле.

Эффект Холла. Тензор магнитосопротивления. Холловская подвижность. Квантование электронов и дырок в сильном магнитном поле. Уровни Ландау. Циклотронный резонанс. Квантовый эффект Холла.

Рассмотрим схему измерений, похожую на ту, что использовалась для измерения удельного сопротивления. Контакты 1 и 2 – токовые контакты, контакты 3-6 потенциальные контакты. В отсутствии магнитного поля, если наш образец однороден по сопротивлению, при пропускании тока через него, падение напряжения между контактами 3 и 5 равно нулю (как и между контактами 4 и 6). В 1879 году, американский физик Э.Холл обнаружил, что если приложить перпендикулярно к образцу магнитное поле, между контактами 3-5 возникает напряжение (Э.Д.С. Холла), пропорциональное току, протекающему через образец. Рассмотрим причины данного эффекта, названного по имени первооткрывателя эффектом Холла.

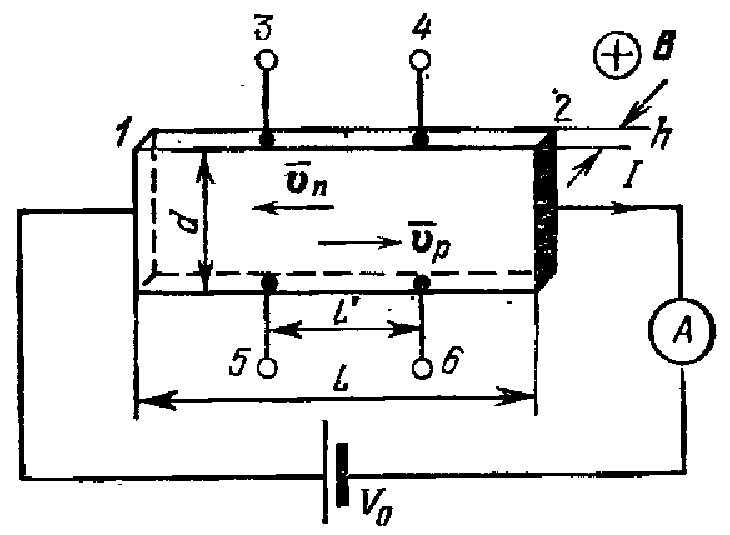
Рис. 6.9. Схема измерения эффекта Холла.

В постоянных электрическом и магнитном полях на заряженную частицу действует сила Лоренца.

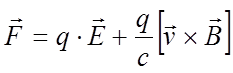
Рассмотрим полупроводник с электронным типом проводимости, концентрация дырок в котором пренебрежимо мала, поэтому их вкладом в ток можно пренебречь. Скорость движения электронов состоит из хаотической тепловой и дрейфовой. В силу линейности силы Лоренца от скорости 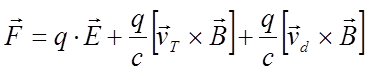. Так как в среднем тепловая скорость равна нулю, то средняя сила зависит только от дрейфовой скорости. Установившийся (после включения магнитного поля) в образце ток течёт слева направо (рис. 6.9), вертикальной компоненты у тока нет. Это происходит из за того, что магнитная составляющая силы Лоренца уравновешивается силой, возникающей из-за Э.Д.С. Холла: 

                  (6.9)

Выразим дрейфовую скорость из формулы 6.7 , где - компонента напряжённости электрического поля, параллельная току. Тогда:

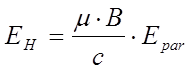
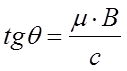                              (6.10)

где  q - угол между направлением тока и направлением электрического поля.

При измерении эффекта Холла важно правильно выбрать геометрию образца и контактов. Металлические контакты 1 и 2 – эквипотенциали на краях образца, на рисунке 6.9 они вертикальны, тогда как в глубине, у контактов 3-6, эквипотенциали наклонены на угол q. Поэтому, для уменьшения искажений, вносимых токовыми контактами, их необходимо удалить от потенциальных контактов. Если угол q мал, то сопротивление образца между контактами 5 и 6 равно: 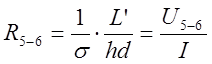, тогда, можно найти удельную проводимость: 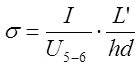. Измеряемая экспериментально Холловская Э.Д.С. равна: 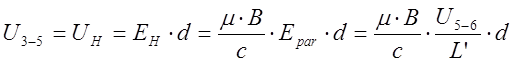. Отсюда подвижность . То есть, измеряя Э.Д.С. Холла можно определить подвижность носителей заряда. Теперь определив подвижность и проводимость, используя можно определить связь между концентрацией носителей заряда и Э.Д.С. Холла: 

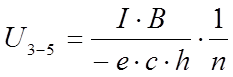                    (6.11)

знак Э.Д.С. Холла направлением магнитного поля и знаком носителей заряда. Постоянную 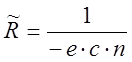 называют коэффициент Холла, или постоянная Холла: 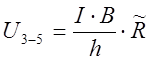. Попробуйте самостоятельно получить, что при учёте дырок с концентрацией p, постоянная Холла равна:

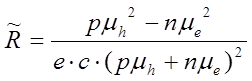                 (6.12)

Как уже отмечалось, влияние магнитного поля приводит к тому, что направлением тока становится не параллельно направлению электрического поля. Проводимость становится тензором: . Удельное сопротивление также становится тензором, в этом случае говорят о тензоре магнитосопротивления. Чтобы точно найти тензор удельного сопротивления (и обратный ему тензор удельной проводимости) нужно найти движение заряженной частицы в скрещенных электрическом и магнитном полях с учётом конечной вероятности её рассеяния (обратно пропорциональной времени релаксации по импульсу). Затем надо усреднить скорость по всему ансамблю частиц, с учётом того что время релаксации зависит от энергии (и от скорости) частицы [2.3]. Качественно, результат заключается в следующем. Недиагональные члены тензора проводимости будут пропорциональны магнитному полю. Диагональные члены тензора проводимости будут чуть меньше, чем в случае отсутствия магнитного поля. Ведь теперь, чтобы сместиться вдоль поля E, частица должна проделать путь больший в 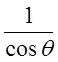 раз.