2.6. Колебательная и вращательная энергии
двухатомных молекул
Как уже отмечалось, различие в массах ядер и электронов дает возможность разделить задачу об определении энергии молекулы. В нулевом приближении находятся уровни энергии системы электронов при неподвижных ядрах, как функция расстояния между последними. Затем можно рассмотреть движение ядер, при заданном электронном состоянии относительно их центра инерции. Поступательное движение центра не представляет интереса и не рассматривается.
Будем
рассматривать первоначально синглетные термы (полный спин S = 0).
Задача о движении двух ядер в поле ![]() , (
, (![]() — центрально-симметричное поле — энергия
электронного терма) сводится к задаче об одномерном движении частицы с
приведенной массой М в эффективном поле, равном сумме
— центрально-симметричное поле — энергия
электронного терма) сводится к задаче об одномерном движении частицы с
приведенной массой М в эффективном поле, равном сумме ![]() и центробежной энергии [1].
и центробежной энергии [1].
Обозначим ![]() сохраняющийся полный момент количества движения
молекулы, включающий орбитальный момент электронов
сохраняющийся полный момент количества движения
молекулы, включающий орбитальный момент электронов ![]() и
момент вращения ядер. Напомним, что орбитальное движение электронов входит в
энергию электронного терма. Поэтому оператор центробежной энергии ядер равен
и
момент вращения ядер. Напомним, что орбитальное движение электронов входит в
энергию электронного терма. Поэтому оператор центробежной энергии ядер равен
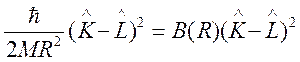 (81)
(81)
Усредняя (81) при заданном R, для эффективной потенциальной энергии получим:
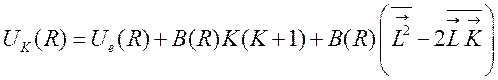 , (82)
, (82)
где 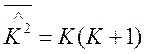 .
.
В орбитальном
моменте отлично от нуля лишь среднее значение проекции ![]() на
ось молекулы
на
ось молекулы ![]() , т.е.
, т.е. ![]() , где
, где ![]() — единичный вектор
в направлении оси молекулы. У системы из двух точечных частиц (ядер) момент
количества движения направлен перпендикулярно оси молекулы, т.е.
— единичный вектор
в направлении оси молекулы. У системы из двух точечных частиц (ядер) момент
количества движения направлен перпендикулярно оси молекулы, т.е. 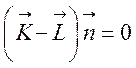 . Следовательно
. Следовательно
![]() ;
(83)
;
(83)
![]() ;
(84)
;
(84)
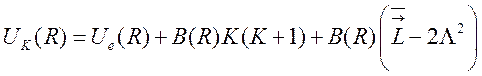 . (85)
. (85)
Видно, что последнее слагаемое в
(85) зависит только от электронной конфигурации, является некоторой функцией R
и может быть включено в ![]() . Таким образом, для
потенциальной энергии окончательно имеем:
. Таким образом, для
потенциальной энергии окончательно имеем:
![]() , (86)
, (86)
где ![]() (согласно
(84)).
(согласно
(84)).
Решение
одномерного уравнения Шредингера для потенциала (86) естественно рассмотреть в
приближении малого смещения относительно положения равновесия ![]() , в котором
, в котором ![]() имеет
минимум. Тогда
имеет
минимум. Тогда
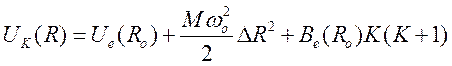 , (87)
, (87)
где ![]() —
частота колебаний молекулы,
—
частота колебаний молекулы, 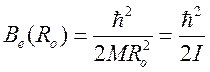 — ротационная
постоянная,
— ротационная
постоянная, ![]() — момент инерции молекулы. В (87) два
слагаемых постоянны, а третий соответствует потенциалу одномерного
гармонического осциллятора. Решение уравнения Шредингера для такого потенциала
хорошо известно:
— момент инерции молекулы. В (87) два
слагаемых постоянны, а третий соответствует потенциалу одномерного
гармонического осциллятора. Решение уравнения Шредингера для такого потенциала
хорошо известно:
![]() , (88)
, (88)
где ![]() = 0,1,2...
= 0,1,2...
Таким образом, в рассматриваемом приближении энергетические уровни складываются из трех независимых частей
![]() ,
,
где:
![]() — отрицательная электронная энергия,
определяющая энергию связи молекулы, включая электростатическое взаимодействие
ядер.
— отрицательная электронная энергия,
определяющая энергию связи молекулы, включая электростатическое взаимодействие
ядер.
![]() при K >
при K > ![]() — положительная энергия ротатора;
— положительная энергия ротатора;
![]() — положительная колебательная энергия.
— положительная колебательная энергия.
Поскольку ![]() , а
, а ![]() , то
, то
![]() :
: ![]() :
: ![]() = 1:
= 1: 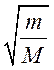 :
: ![]() .
.
Таким образом, распределение энергетических уровней молекулы имеет сложный характер. Колебательное движение расщепляет электронные термы, а вращательное движение, в свою очередь, осуществляет еще более тонкое расщепление каждого электронно-колебательного состояния.
В следующих приближениях разделение на чисто вращательную и колебательную энергии становится невозможным. Они начинают зависеть друг от друга. При сильных колебаниях необходимо учитывать ангармонизм [1].
Рассмотрим кратко классификацию молекулярных термов с отличным от нуля спином S. Здесь включается процесс, которым мы пренебрегали при анализе молекул-спин-орбитальное взаимодействие.
Возможны два
случая: в одном из них энергия спин-орбитального взаимодействия ![]() велика по сравнению с разностью между
двумя вращательными уровнями
велика по сравнению с разностью между
двумя вращательными уровнями ![]() (а), в другом — мала
(б).
(а), в другом — мала
(б).
Рассуждения, аналогичные приведенным выше, позволяют получить выражение для энергии в случае “а” [1]
![]() , (89)
, (89)
где J — полный момент
молекулы, включающий орбитальный и спиновый моменты электронов и момент
вращения ядер (![]() ).
). 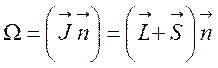 —
проекция момента на ось молекулы. Момент вращения ядер перпендикулярен оси.
—
проекция момента на ось молекулы. Момент вращения ядер перпендикулярен оси. ![]() — энергия спин-орбитального
взаимодействия, дополнительное слагаемое, которое отсутствует в (88). Отметим,
что в случае (а)
— энергия спин-орбитального
взаимодействия, дополнительное слагаемое, которое отсутствует в (88). Отметим,
что в случае (а) ![]() (полный момент молекулы без
учета спина) не сохраняется даже приближенно, тогда как в случае (б) мы имеем
(полный момент молекулы без
учета спина) не сохраняется даже приближенно, тогда как в случае (б) мы имеем ![]() и для нахождения энергии без учета
спин-орбитального взаимодействия можно использовать выражение (88).
и для нахождения энергии без учета
спин-орбитального взаимодействия можно использовать выражение (88).
Спин-орбитальная добавка имеет вид оператора, который должен быть усреднен по электронному и вращательному состояниям при заданном R (расстоянии между ядрами).
Согласно [1], для этой добавки получим
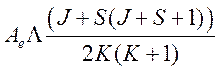 ,
,
где ![]() —
некоторая функция расстояния между ядрами при R =
—
некоторая функция расстояния между ядрами при R = ![]() .
.
Оценим порядок
величин колебательной и вращательной энергии. Например, молекула СО имеет
приведенную массу ![]() кг, расстояние между атомами
0,113 нм и
кг, расстояние между атомами
0,113 нм и ![]() . Минимальная энергия вращения (J = 1)
равна
. Минимальная энергия вращения (J = 1)
равна 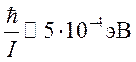 . Угловая
скорость вращения
. Угловая
скорость вращения 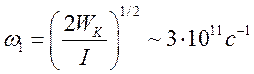 . Напомним, что при комнатной
температуре
. Напомним, что при комнатной
температуре ![]() , что в
, что в ![]() раз больше кванта вращательной
энергии.
раз больше кванта вращательной
энергии.
Колебательная
энергия молекулы СО ![]() и частота колебаний
и частота колебаний ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.