Соотношения
(2.11 ![]() 2.13) служат отправным пунктом для
нахождения сечения поглощения и излучения фотона атомной системой [5].
2.13) служат отправным пунктом для
нахождения сечения поглощения и излучения фотона атомной системой [5].
Коэффициент
поглощения ![]() (или усиления
(или усиления ![]() ),
который характеризует вероятность поглощения (или испускания) кванта света на
единице длины пути, равен
),
который характеризует вероятность поглощения (или испускания) кванта света на
единице длины пути, равен
![]() (3.1)
(3.1)
где ![]() и
и ![]() – концентрация атомов на верхнем i и нижнем f уровнях атома.
– концентрация атомов на верхнем i и нижнем f уровнях атома.
Величины ![]() могут быть найдены из условия
термодинамического равновесия излучения и атомов в возбужденном состоянии.
Сечение равно отношению вероятности индуцированного излучения в единицу
времени, рассчитанной квантовомеханическим методом в п. 2, к классической
плотности потока фотонов.
могут быть найдены из условия
термодинамического равновесия излучения и атомов в возбужденном состоянии.
Сечение равно отношению вероятности индуцированного излучения в единицу
времени, рассчитанной квантовомеханическим методом в п. 2, к классической
плотности потока фотонов.
Плотность
потока фотонов, приходящаяся на единичный интервал частот ![]() , найдем из следующих условий. Энергия
электромагнитного поля в объеме V, по классике,
равна
, найдем из следующих условий. Энергия
электромагнитного поля в объеме V, по классике,
равна ![]() С другой стороны, она равно произведению
энергии фотона
С другой стороны, она равно произведению
энергии фотона ![]() и среднего их числа с данной
частотой
и среднего их числа с данной
частотой ![]() , умноженному на число состояний
, умноженному на число состояний ![]() и
и ![]() – число
состояний поляризации, т.е.
– число
состояний поляризации, т.е.
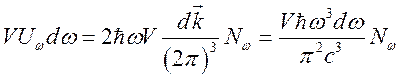
Следовательно,
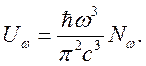 (3.2)
(3.2)
Используя классическую и квантовую запись вероятности вынужденного излучения
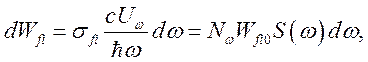
с учетом (3.2), для сечения вынужденного излучения получим
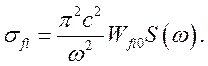 (3.3)
(3.3)
Учитывая (2.13), для сечения поглощения получим
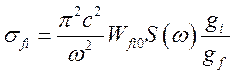 (3.4)
(3.4)
и
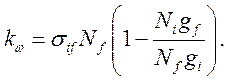 (3.5)
(3.5)
Максимум сечения
![]() Если атомы находятся в термодинамическом
равновесии, то
Если атомы находятся в термодинамическом
равновесии, то
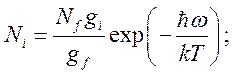
![]()
и коэффициент поглощения равен
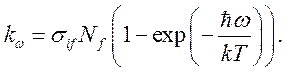
Если ![]() , что возникает только при нарушении
термодинамического равновесия, то система будет усиливать свет, т.е. в среде
возможен эффект лазерной генерации. Создание инверсии, т.е. повышенной
заселенности верхнего уровня, или условий с “отрицательной” температурой
возможно при реализации механизма селективного возбуждения этого уровня.
, что возникает только при нарушении
термодинамического равновесия, то система будет усиливать свет, т.е. в среде
возможен эффект лазерной генерации. Создание инверсии, т.е. повышенной
заселенности верхнего уровня, или условий с “отрицательной” температурой
возможно при реализации механизма селективного возбуждения этого уровня.
Активная среда
расположена между двумя плоскими зеркалами с коэффициентами отражения ![]() и
и ![]() ,
расстоянием между зеркалами L. Такая оптическая
система называется резонатором типа Фабри-Перо. В таком резонаторе при малых
потерях
,
расстоянием между зеркалами L. Такая оптическая
система называется резонатором типа Фабри-Перо. В таком резонаторе при малых
потерях ![]() возможно установление стационарного поля
излучения, практически равномерного вдоль оси и спадающего в зависимости от
расстояния от оси по закону
возможно установление стационарного поля
излучения, практически равномерного вдоль оси и спадающего в зависимости от
расстояния от оси по закону ![]() , где
, где ![]() . Тогда уравнение баланса для плотности
фотонов с частотой
. Тогда уравнение баланса для плотности
фотонов с частотой ![]() :
:
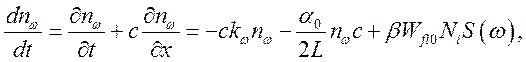
где второе слагаемое в правой
части уравнения учитывает потери фотонов за счет ухода из системы ![]() а
а ![]() -
вероятность спонтанного излучения фотона внутрь резонатора. Принято
-
вероятность спонтанного излучения фотона внутрь резонатора. Принято ![]() . Условие возникновения генерации, т.е.
усиления числа фотонов внутри резонатора:
. Условие возникновения генерации, т.е.
усиления числа фотонов внутри резонатора:
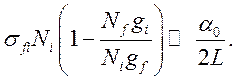 (3.9)
(3.9)
В этом случае число
фотонов нарастает, увеличивается роль вынужденного излучения, что приводит к изменению
заселенности энергетических состояний i и f, т.е. величины ![]() и
и ![]() изменяются:
изменяются:
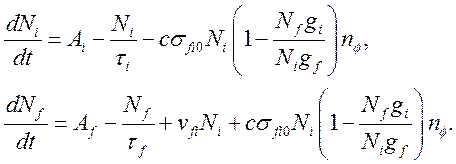 (3.10)
(3.10)
Здесь ![]() и
и ![]() – скорости
возбуждения атомов на i и
f уровнях,
– скорости
возбуждения атомов на i и
f уровнях, ![]() – времена жизни,
определяемые как собственным временем жизни, так и столкновениями,
– времена жизни,
определяемые как собственным временем жизни, так и столкновениями, ![]() – полная частота переходов с i на f
уровень, в результате столкновений и спонтанного излучения. Усиление света
максимально в центре линии. Поэтому формируемая в резонаторе волна одной моды
имеет спектральную ширину много меньше ширины линии перехода. Учитывая данное
обстоятельство, излучение лазера можно считать монохроматическим с плотностью
фотонов
– полная частота переходов с i на f
уровень, в результате столкновений и спонтанного излучения. Усиление света
максимально в центре линии. Поэтому формируемая в резонаторе волна одной моды
имеет спектральную ширину много меньше ширины линии перехода. Учитывая данное
обстоятельство, излучение лазера можно считать монохроматическим с плотностью
фотонов ![]() , усиливаемых в центре линии, т.е.
, усиливаемых в центре линии, т.е. ![]()
Пренебрегая ![]() и решая систему (3.10), для стационарного режима
получим
и решая систему (3.10), для стационарного режима
получим
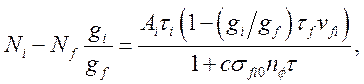 (3.11)
(3.11)
где
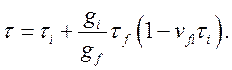
Как видно, под
действием поля излучения инверсия заселенности уровней снижается, так что
коэффициент усиления k в
действующем лазере меньше коэффициента усиления ![]() в
отсутствии поля излучения:
в
отсутствии поля излучения:
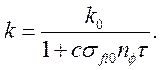 (3.12)
(3.12)
Здесь принято, что ![]() .
.
Рассмотрим
нестационарные процессы в лазере. Для простоты анализа положим ![]() ,
, ![]() и
и ![]() , что позволяет решить задачу (3.10) для
разности заселенности
, что позволяет решить задачу (3.10) для
разности заселенности ![]()
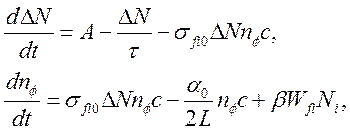 (3.13)
(3.13)
где ![]()
Предположим,
что в начальный момент система имела возбужденные атомы, однако плотность
фотонов определялась только спонтанным излучением (режим модулированной
добротности). Практически это может быть достигнуто введением в резонатор
сильного поглощения, т.е. ![]() велико
велико ![]() . Если очень быстро уменьшить поглощение,
то начнётся развитие генерации. При этом начальное значение
. Если очень быстро уменьшить поглощение,
то начнётся развитие генерации. При этом начальное значение ![]() и
и ![]() –
мало, так что усиление числа фотонов описывается уравнением:
–
мало, так что усиление числа фотонов описывается уравнением:
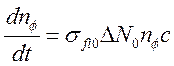
![]() (3.14)
(3.14)
где ![]() –
коэффициент усиления света на единицу длины. Плотность фотонов, при которой
начинается изменение
–
коэффициент усиления света на единицу длины. Плотность фотонов, при которой
начинается изменение ![]() , равна
, равна
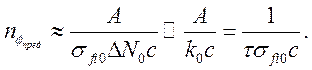 (3.15)
(3.15)
Если эта
плотность достигается за время прохода фотона от одного зеркала до другого ![]() то такой режим работы называется
суперлюминесцентным, т.е. высокий уровень мощности света
то такой режим работы называется
суперлюминесцентным, т.е. высокий уровень мощности света
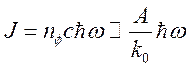
достигается в отсутствии зеркал и
может быть реализован, учитывая (3.14), при большом коэффициенте усиления ![]() .
.
Второй
предельный случай малого ![]() требует большего числа
проходов света между зеркалами для достижения предельной плотности фотонов:
требует большего числа
проходов света между зеркалами для достижения предельной плотности фотонов:
![]() ,
,
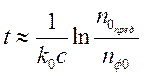 , (3.16)
, (3.16)
где ![]()
Установившиеся
плотности фотонов ![]() и
и ![]() определяются
из системы уравнений:
определяются
из системы уравнений:
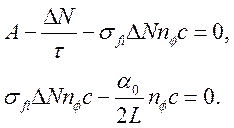 (3.17)
(3.17)
Откуда
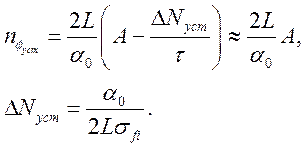 (3.18)
(3.18)
Мощность
излучения через единицу площади одного зеркала с пропусканием ![]() равна
равна 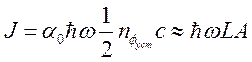 , а
условия на
, а
условия на ![]() соответствуют равенству усиления потерям.
Учет релаксационных потерь приводит к оценке мощности:
соответствуют равенству усиления потерям.
Учет релаксационных потерь приводит к оценке мощности:
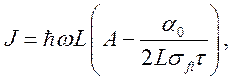 (3.19)
(3.19)
где ![]() и
и ![]()
Коэффициент полезного действия лазера равен:
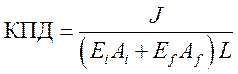 (3.20)
(3.20)
и отличается от “квантового”, т.е. идеального
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.