Молекулы. Ковалентная связь (Раздел 2-2.1. учебного пособия)

2. Молекулы

Молекулой называется стабильное объединение двух и более атомов [1,2,6]. Для распада молекулы необходимо затратить энергию, равную энергии связи. В теории молекул основную роль играет тот факт, что масса ядер атомов существенно больше массы электронов. Это дает возможность рассматривать электронное движение при неподвижных ядрах, расположенных на заданном расстоянии друг от друга. Хотя молекула и состоит из электрически нейтральных атомов, силы, удерживающие атомы являются электростатическими по своей природе. Когда говорится об электронной энергии или электронных термах молекулы, предполагаются уровни энергии электронного движения при неподвижных ядрах, к которым добавляется энергия взаимодействия ядер.

Физический механизм связи может быть различен, однако, можно выделить два предельных случая:

- ковалентная связь, когда один или большее число электронов становится общими для двух (или более) атомов. Например, молекула .

- ионная связь, когда один или большее число электронов переходят от  одного атома к другому и возникающие положительные и отрицательные ионы притягиваются (например, NaCl).

Встречается много молекул и с промежуточной системой связи, что позволяет рассматривать ионную связь, как предельный случай ковалентной связи.

2.1. Ковалентная связь

Простейшей молекулярной системой является молекулярный ион водорода , в котором два протона связаны единственным электроном.

Возникновение стабильной системы  легко понять на качественном уровне, если привлечь квантовомеханические представления. Действительно, два протона образуют для электрона две потенциальные ямы со стенкой между ними (см. рис. 12).

В классической физике нет механизма, обуславливающего переход электрона из одной ямы в другую. Расчеты с учетом квантовомеханического туннелирования показывают, что если сблизить протоны до расстояния ~ 1 , то электрон переходит из одной ямы в другую ~  раз в секунду. При

увеличении расстояния до 10  перемещение электрона уменьшается до одного раза в секунду. Поскольку эффективный радиус волновой функции 1s равен 0,53 , то можно сказать, что обобществление электронов возможно при перекрытии волновых функций.

 

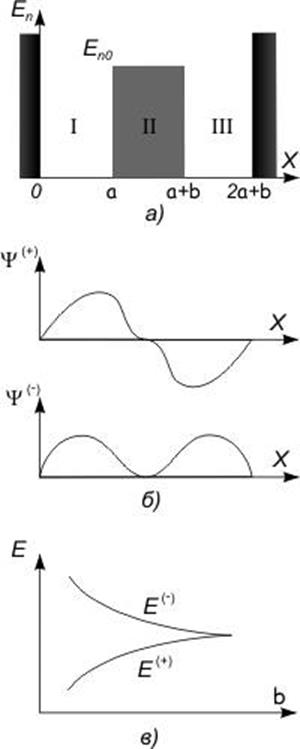
Согласно принципу неопределенности, чем меньше область движения электрона, тем больше его импульс, а, следовательно, и кинетическая энергия. Поэтому при увеличении пространства за счет двух протонов кинетическая энергия электрона в ионе  оказывается меньше, чем в системе Н + . Кроме этого, отрицательная энергия электростатического взаимодействия электрона по модулю возрастает за счет взаимодействия со вторым протоном. Если это уменьшение энергии электрона превышает дополнительную положительную энергию взаимодействия двух протонов, то ион  оказывается стабильным.

В принципе, задача о нахождении энергии связи иона  в приближении неподвижных ядер может быть решена точно. Однако, учитывая сложность и громоздкость вычислений, здесь будет использован приближенный метод орбиталей. Сущность его состоит в том, что в качестве волновой функции молекулы берется суперпозиция атомных волновых функций  и , где a и b — обозначения протонов.

Волновая функция, характеризующаяся квантовыми числами n, l,  называется атомной орбиталью. На каждой орбитали может находится два электрона с противоположными ориентациями спинов . Молекулярная орбиталь строится из атомных для водорода в 1s состоянии следующим образом:

 -                                        (49)

симметричная комбинация и

 -                                       (50)

антисимметричная комбинация.

Условия нормировки

сводятся к нахождению нормировочных констант  и , где  — называется интегралом перекрытия. Интегрирование проводится по всему пространству. Расчет с использованием явного вида  [2] в состоянии 1s дает

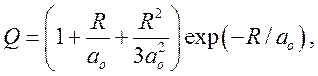
где  — боровский радиус, R — расстояние между протонами (рис.13).

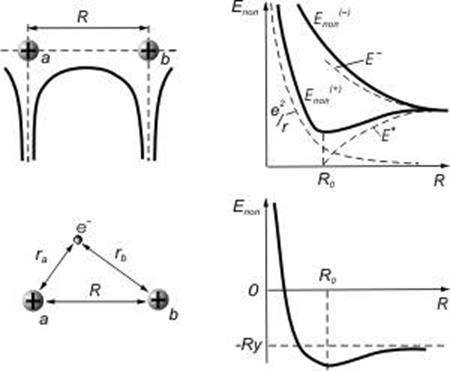
Для нахождения энергии электрона в молекуле  необходимо решить уравнение Шредингера

,                               (51)

где  и  — расстояние электрона от протонов а и b выражено в единицах 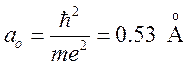, а энергия — в единицах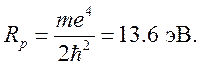  

Процедура решения уравнения (51) упрощается, так как мы знаем приближенные волновые функции. Тогда переписав (51) в виде