1. АТОМЫ
В нерелятивистском приближении стационарные состояния атома определяются уравнением Шредингера для системы электронов, движущихся в кулоновском поле ядра и электрически взаимодействующих друг с другом [1]
![]() , (1)
, (1)
где ![]() —
оператор Гамильтона и
—
оператор Гамильтона и ![]() — собственная волновая функция,
описывающая состояние атома. Для атома, имеющего ядро с зарядом +Ze и N
электронов, гамильтониан можно представить в виде суммы:
— собственная волновая функция,
описывающая состояние атома. Для атома, имеющего ядро с зарядом +Ze и N
электронов, гамильтониан можно представить в виде суммы: 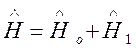 , где:
, где:
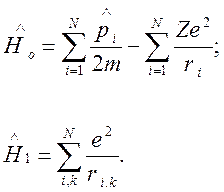 (2)
(2)
Здесь ![]() —
добавка, связанная со взаимодействием электронов между собой,
—
добавка, связанная со взаимодействием электронов между собой, ![]() — расстояние i-го электрона от
ядра,
— расстояние i-го электрона от
ядра, ![]() — расстояние между i и k-электронами
(суммирование в операторе
— расстояние между i и k-электронами
(суммирование в операторе ![]() проводится по всем
проводится по всем ![]() ).
).
В это уравнение не входят операторы спина электронов. В действительности, однако, всегда существует некоторое релятивистское электромагнитное взаимодействие электронов, зависящее и от их спинов. Поэтому гамильтониан должен быть дополнен членом, учитывающим подобные взаимодействия:
![]()
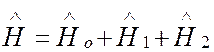 , (3)
, (3)
где ![]()
![]() включает спин-орбитальное и спин-спиновое
взаимодействия электронов.
включает спин-орбитальное и спин-спиновое
взаимодействия электронов.
Прежде всего,
целесообразно проанализировать решение задачи (1), используя метод
последовательных приближений, считая, что 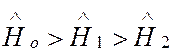 . Это
позволит выявить основные процессы, определяющие энергию атома.
. Это
позволит выявить основные процессы, определяющие энергию атома.
В нулевом приближении решение задачи:
![]() (4)
(4)
найдем в виде произведения N волновых функций, каждая из которых зависит от координат соответствующего электрона
![]()
![]() (5)
(5)
Учет влияния тождественности электронов и симметрии Y будет рассмотрен ниже (разд. 1.2).
Принимая во
внимание, что функции ![]() независимы друг от друга,
уравнение (4), с учетом (2), может быть записано в виде системы уравнений:
независимы друг от друга,
уравнение (4), с учетом (2), может быть записано в виде системы уравнений:
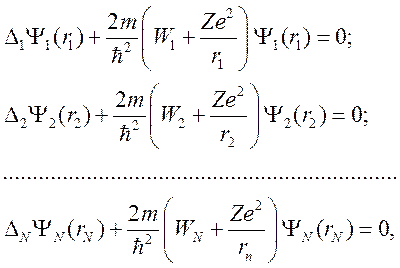 (6)
(6)
где 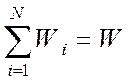 .
.
Уравнения системы (6) совпадают с уравнением Шредингера для водорода и водородоподобных ионов с зарядом Z.
Таким образом, в нулевом приближении задача о расчете состояния сложного атома сводится к нахождению энергии водородоподобного иона с зарядом ядра Z и одним электроном. Энергия атома равна сумме энергий всех электронов.
Рассмотрим, насколько такое приближение соответствует опытным данным, на примере простейшего сложного атома — атома гелия. Энергия связи электрона в атоме с зарядом ядра Z = 2 равна 54,40 эВ. Следовательно, энергия, необходимая для двукратной ионизации He, составит 108,80 эВ. В действительности, она равна 78,98 эВ, т.е. на ~ 30% меньше. Это указывает на важную роль процессов взаимодействия электронов между собой, то есть необходимость учета следующих членов в гамильтониане (2).
Однако
нулевого приближения оказывается достаточно для описания электронной
конфигурации атомов, особенно легких. Как мы знаем [1], для системы частиц
в центрально-симметричном внешнем поле сохраняется полный орбитальный момент ![]() , а также четность состояния. Кроме этого,
координатные волновые функции стационарных состояний системы тождественных
частиц обладают определенной перестановочной симметрией, которой соответствует
определенное значение полного спина системы.
, а также четность состояния. Кроме этого,
координатные волновые функции стационарных состояний системы тождественных
частиц обладают определенной перестановочной симметрией, которой соответствует
определенное значение полного спина системы.
Состояние
электрона в атоме, в рассматриваемом приближении, характеризуется четырьмя
квантовыми числами, которые подробно рассматривались при анализе атома водорода [1]:
n - главное квантовое число, ![]() — орбитальный момент,
— орбитальный момент, ![]() — его проекция и
— его проекция и ![]() —
проекция спина электрона. Орбитальный момент и полный спин атома определяются
выражениями
—
проекция спина электрона. Орбитальный момент и полный спин атома определяются
выражениями 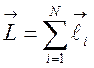 и
и 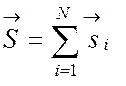 .
Полный момент атома
.
Полный момент атома 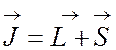 . При заданном n значения
квантовых чисел равны
. При заданном n значения
квантовых чисел равны ![]()
![]() .
.
В соответствии
с принципом Паули, никакие два электрона не могут находиться в одном и том же
квантовом состоянии, определяемом квантовыми числами n, ![]() ,
, ![]() ,
, ![]() .
.
Электроны, имеющие одинаковое число n образуют оболочку
|
n |
1 |
2 |
3 |
4 |
5 |
|
Обозначение оболочки |
K |
L |
M |
N |
O |
Число электронов в оболочке
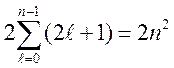 ,
,
множитель 2 учитывает две ориентации спина.
Электроны с
заданными значениями ![]() и
и ![]() образуют
подоболочку, в которой может находиться
образуют
подоболочку, в которой может находиться ![]() частиц.
частиц.
Состояние
отдельных электронов с различными ![]() и
и ![]() принято обозначать символом, состоящим из
цифры, указывающей значение n и буквы, указывающей значение
принято обозначать символом, состоящим из
цифры, указывающей значение n и буквы, указывающей значение ![]() :
:
|
|
0 |
1 |
2 |
3 |
|
Обозначение подоболочки |
s |
p |
d |
|
Например, для
натрия имеем: ![]() . Эта запись обозначает, что
. Эта запись обозначает, что ![]() и
и ![]() содержат
по 2 электрона,
содержат
по 2 электрона, ![]() — 6 электронов и
— 6 электронов и ![]() — 1 электрон.
— 1 электрон.
Состояния всего атома (или, как часто говорят, спектральные термы атомов) принято обозначать символами, аналогичными тем, которые используются для обозначения состояний отдельных электронов с определенным значением момента
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.