Атомы. Энергетические уровни атомов с одним электроном в верхней оболочке (Раздел 1-1.1. учебного пособия), страница 2

L =  0     1     2     3     4     5     6

                                            S     P    D    F     G    H     I

Слева вверху от этого символа указывается число , называемое мультиплетностью терма, а справа внизу — значение полного момента. Так  — означает уровни с   и .

Еще  раз подчеркнем, что рассмотренная методика построения электронных конфигураций атома основана на нулевом приближении решения уравнения Шредингера (1), учитывает наличие спина у электрона и принцип Паули.

Эффективность данного подхода, а также его ограниченность будут рассмотрены ниже  (в разделе), а также при анализе последовательности заполнения электронных оболочек, т.е. формировании периодической системы (Д.И.Менделеева).

1.1. Энергетические уровни атомов с одним

электроном в верхней оболочке

Атом водорода является единственной системой, для которой уравнение Шредингера может быть решено точно. Уровни энергии атома водорода и сходных с ним ионов  , содержащих всего по одному электрону, определяются формулой Бора:

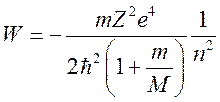,                                        (7)

где Ze, M - заряд и масса ядра. Энергетические уровни  раз вырождены.

В атомах щелочных металлов и в сходных с ними ионах один электрон движется вокруг атомного остова с полностью заполненными внутренними электронными оболочками, для которых выполняются условия L = 0 и S = 0, т.е. данный остов должен обладать сферической симметрией. Естественно предположить, что заряд электронов остова частично компенсирует заряд ядра и потенциальная энергия взаимодействия в (2) может быть записана в виде [2,3]:

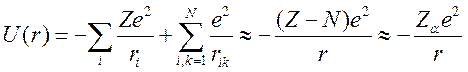,                     (8)

где  — эффективный заряд иона остова.

Внешний электрон, взаимодействуя с остовом, может обусловить его поляризацию. Разлагая поле остова по моментам и учитывая только дипольную составляющую для потенциальной энергии, получим:

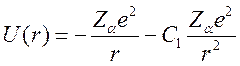,                                         (9)

где  — постоянная, характеризующая величину дипольного момента.

При таком потенциале угловые функции уравнения Шредингера остаются теми же, что и в случае атома водорода, а радиальная часть уравнения имеет вид:

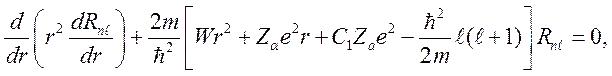        (10)

который совпадает с уравнением для водорода, если положить

,             

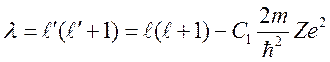где  — величина равная:

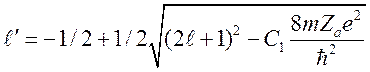.                          (11)

Предполагая  малой, получим

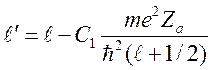.                                          (12)

Таким образом, уравнение Шредингера для радиальных функций сведено к виду, для которого хорошо известно решение для энергии:

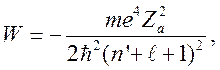                                           (13)

где вместо главного квантового числа  необходимо поставить  или

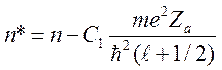.                                          (14)

Следовательно, энергия уровней равна:

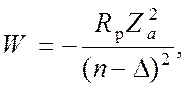                                                (15)

где  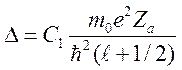зависит от , .

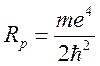Как видно из (15), энергетические состояния с малым  возмущаются сильнее, а с ростом   квантовый дефект  стремится к нулю, и энергетические состояния близки к водородным.

Таким образом, учет электростатического взаимодействия электрона с полем внутренних электронов, проведенный нами в виде возмущения дипольного типа, приводит к снятию вырождения по . Состояние с заданным n распадается на n состояний, соответствующих различным значениям . Кроме этого, как будет показано в разделе 1.3, все термы расщепляются на два за счет спин-орбитального взаимодействия.

На рис.1, в качестве примера, приведена схема энергетических уровней натрия. Для сравнения там же приведены энергетические уровни водорода. Приведенная схема наглядно иллюстрирует зависимость энергии атома натрия от главного квантового числа n и орбитального  электрона в верхней оболочке. Энергии связи электрона в атоме водорода равны:  и . Тогда как в Na энергии связи 3S электрона  и  и только у 3d электрона , т.е. близка к уровню энергии атома водорода в состоянии с n = 3.  Из приведенных данных видно, что изменение энергии за счет  при n = 3 в атоме Na больше, чем изменение энергии за счет роста n (c n = 2 до n = 3) в атоме водорода.

С увеличением атомного веса щелочного металла возрастает главное квантовое число n и величина дефекта  наиболее глубокого S-терма (см. таблицу 1).

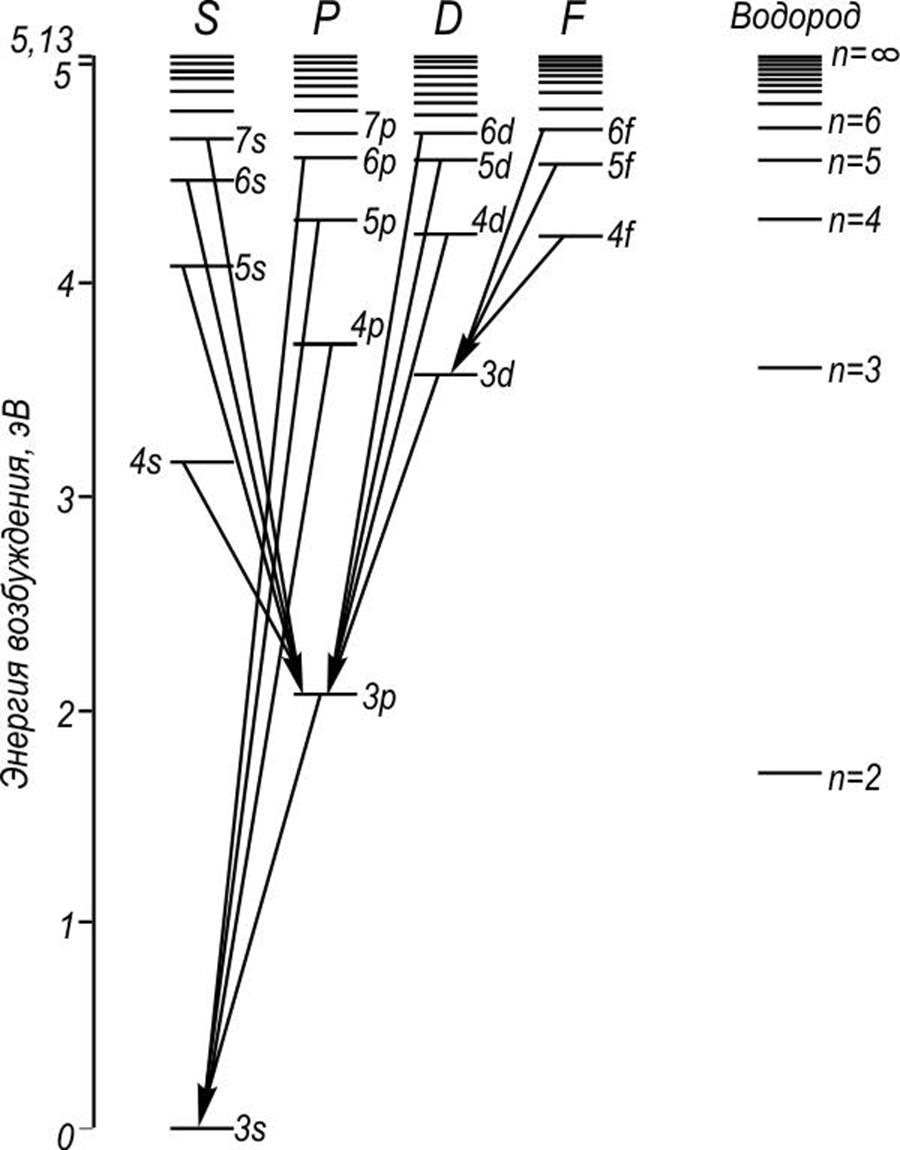
Таблица 1

Элемент	n
Li	2	0,41
Na	3	1,37
K	4	2,23
Rb	5	3,20
Gs	6	4,13

Для данного элемента и данного  квантовый дефект  практически не зависит от n, в полном соответствии с (14).