Взаимодействие излучения с атомами и молекулами (Раздел 3 учебного пособия)

3. Взаимодействие излучения с атомами и молекулами

Поскольку характерная скорость электрона в атомах (молекулах) много меньше скорости света, то в нулевом приближении атомную систему и электромагнитное поле можно считать невзаимодействующими, а их взаимодействие, приводящее к переходам между дискретными состояниями, рассматривать в рамках теории возмущений. При этом малым параметром теории возмущений является отношение скорости электрона к скорости света.

Размер водородоподобного атома с зарядом ядра Z равен , а скорость электрона в атоме

,

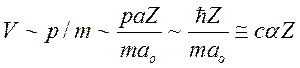то есть релятивистские эффекты необходимо учитывать для тяжелых ядер . В данных оценках использованы обозначения: 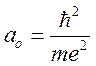 — боровский радиус, 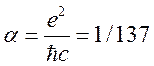 — постоянная тонкой структуры. При переходе с уровня с главным квантовым числом n₁ на уровень с   электрон излучает частоту

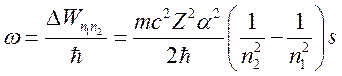                          (123)

того же порядка, что и классическая частота обращения электрона на орбите

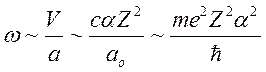.                              (124)

При этом длина волны излучения оказывается существенно больше размеров атома

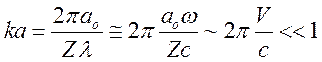                           (125)

при .

3.1. Вероятность излучения и поглощения фотона атомной системой в единицу времени

Взаимодействие электронов с электромагнитным полем будет учтено, если в гамильтониане атомной системы оператор импульса каждого из электронов  заменить разностью  обобщенного импульса, ( — векторный потенциал). В результате гамильтониан взаимодействующих атомной системы и поля представится в виде

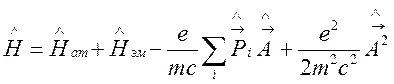,                    (126)

где  и  — гамильтонианы невзаимодействующих атомной системы и поля, соответственно, а два последних слагаемых характеризуют взаимодействие между этими системами; i — суммирование по всем электронам.

В [5] показан вывод вероятности излучения атома на основе классической формулы для интенсивности дипольного излучения двигающегося электрона. Такой подход возможен (с учетом (123-125)), строго говоря, для переходов с большими квантовыми числами , когда в рамках принципа соответствия Бора матричные элементы, рассчитанные в квазиклассическом приближении, переходят в компоненты Фурье классических величин (см. § 48 [1]).

Однако, полученная формула оказывается применима для любых переходов, то есть в данном частном случае принцип соответствия оказывается справедливым в общем случае [4].

Здесь мы кратко рассмотрим вывод вероятности излучения, используя квантование электромагнитного поля, так называемое, вторичное квантование. Подробнее с данной проблемой можно ознакомиться в литературе (см., например [4]).

Чтобы рассмотреть поле, как квантовый объект, удобно исходить из такого классического описания поля, в котором оно характеризуется хотя и бесконечным, но дискретным набором переменных. Для этого заключим нашу атомную систему и поле в ящик объемом W так, что размеры этого ящика много больше любых других характерных размеров. Разложим векторный потенциал по плоским волнам

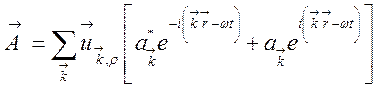,                     (127)

где  — единичный вектор, индекс  характеризует поляризацию волны,  и  - волновой вектор и частота волны.

В отсутствии взаимодействия электромагнитное поле можно представить как набор невзаимодействующих гармонических осцилляторов, каждый из которых включает в себя фотон с определенным волновым вектором  и частотой .

Действительно, перепишем (127) в виде

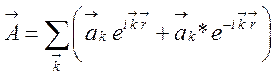,                             (128)

где коэффициенты  зависят от времени по закону 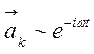, ортогональны к , то есть 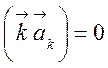, что обусловлено поперечностью электромагнитной волны. Суммирование проводится по бесконечному дискретному набору волновых векторов (его трех компонент).

Введем канонические переменные для поля:

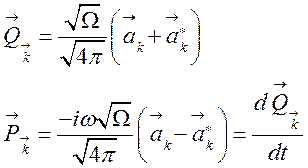,                                   (129)

Векторный потенциал запишется через канонические переменные

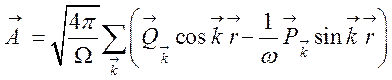.                  (130)

Функция Гамильтона  для электромагнитного поля

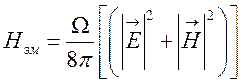,                               (131)

где 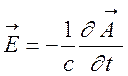, , 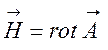. Выразив  из (130) и подставив в (131), получим

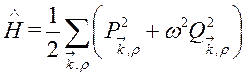.                             (132)

Здесь и далее двухкомпонентные вектора 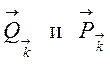 записываются в ви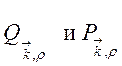де: , где  — суммирование по двум компонентам векторов, лежащим в плоскости, перпендикулярной .