3.4. Изменение скорости спонтанного излучения атома
в замкнутом пространстве
Согласно [1]
скорость спонтанного распада возбужденного состояния атома пропорциональна
плотности мод электромагнитного поля на частоте атомного перехода ![]()
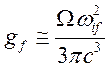 ,
(175)
,
(175)
где ![]() — объем
пространства.
— объем
пространства.
Если атом
находится не в свободном пространстве, для которого ![]() , а
например, в резонаторе, то континуум мод превращается в спектр дискретных мод,
одна из которых может быть в резонансе с атомом. Скорость спонтанного излучения
атома в этом случае будет уже определяться плотностью осцилляторов
электромагнитного поля в моде резонатора
, а
например, в резонаторе, то континуум мод превращается в спектр дискретных мод,
одна из которых может быть в резонансе с атомом. Скорость спонтанного излучения
атома в этом случае будет уже определяться плотностью осцилляторов
электромагнитного поля в моде резонатора
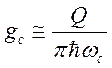 ,
(176)
,
(176)
где ![]() —
добротность,
—
добротность, ![]() — собственная частота резонатора.
— собственная частота резонатора.
Таким образом, выражение для вероятности спонтанного перехода (141) должно быть переписано в виде
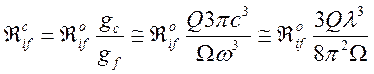 , (177)
, (177)
где использовано ![]() и
и ![]() .
Формула (177) предсказывает значительное увеличение вероятности спонтанного
распада при переходе от cвободного пространства к высокодобротному резонатору,
когда длина волны сравнима с линейными размерами резонатора. Например, при
.
Формула (177) предсказывает значительное увеличение вероятности спонтанного
распада при переходе от cвободного пространства к высокодобротному резонатору,
когда длина волны сравнима с линейными размерами резонатора. Например, при ![]() ,
, ![]() , т.е.
может возрастать примерно в
, т.е.
может возрастать примерно в ![]() раз.
раз.
Однако, если резонатор расстроен
(![]() , можно ожидать, что вероятность излучения
должна уменьшиться, то есть атом не может излучить фотон, поскольку резонатор
не в состоянии его принять.
, можно ожидать, что вероятность излучения
должна уменьшиться, то есть атом не может излучить фотон, поскольку резонатор
не в состоянии его принять.
Для того,
чтобы изменить скорость распада атомного состояния, наличие резонатора не обязательно.
Любая проводящая поверхность вблизи излучателя влияет на плотность мод
и, следовательно, на скорость спонтанного излучения. В экспериментах, в
которых наблюдается рост спонтанного излучения, большое число атомов в объеме ![]() может исказить эксперимент вследствие
возможного вынужденного излучения. Поэтому в подобных опытах используется
система с одним атомом в объеме
может исказить эксперимент вследствие
возможного вынужденного излучения. Поэтому в подобных опытах используется
система с одним атомом в объеме ![]() резонатора [9]
резонатора [9]
.
Эксперименты, в которых подавляется спонтанное излучение, могут быть проведены и с большим числом атомов. Так, подавление спонтанного излучения впервые наблюдалось в тонкой пленке красителя, нанесенного на поверхность зеркала. Благодаря образованию конфигурации стоячих волн вблизи поверхности при интерференции падающей и отраженной волн, наблюдалось уменьшение вероятности спонтанного распада [9].
В
экспериментах [9] наблюдалось увеличение
вероятности спонтанного излучения высоковозбужденных атомов Na (главное квантовое
число ![]() ), помещенных в ниобиевый
сверхпроводящий резонатор с добротностью
), помещенных в ниобиевый
сверхпроводящий резонатор с добротностью ![]() .
Переходы между уровнями с большим n имеют большую длину волны, что облегчает
возможность выполнения условия
.
Переходы между уровнями с большим n имеют большую длину волны, что облегчает
возможность выполнения условия ![]() .
.
Таким образом, к настоящему времени имеется широкий набор экспериментальных данных, подтверждающих факт влияния ограниченного объема на спонтанное излучение (см. например, обзоры [10,11]).
Следуя работе [9], мы рассмотрим теорию спонтанного излучения в ограниченных объемах. Для краткости изложения все промежуточные выкладки будут опущены. Читатель может ознакомиться с ними в [9].
Рассматривается следующая модель (Вайскопфа-Вигнера): двухуровневый атом взаимодействует с осциллятором поля, который в свою очередь взаимодействует с системой, имеющей непрерывный спектр поглощения. Осциллятор описывает моду резонатора, ближайшую по частоте с двухуровнему атому. Взаимодействие осциллятора с системой с непрерывным спектром (стенки резонатора) учитывает затухание электромагнитной волны в резонаторе.
Гамильтониан такой сложной системы имеет вид:
![]() , (178)
, (178)
где ![]() —
собственная энергия атома,
—
собственная энергия атома, ![]() — энергия осциллятора,
— энергия осциллятора, ![]() — энергия поглощающей системы (стенок
резонатора),
— энергия поглощающей системы (стенок
резонатора), ![]() — потенциал взаимодействия атома с
осциллятором,
— потенциал взаимодействия атома с
осциллятором, ![]() — взаимодействие осциллятора с
поглотителем. Состояние совокупной системы описывается тремя индексами ôа, с, wñ. Первый индекс указывает на состояние
атома, второй осциллятора, третий — стенок. Возможны три основные состояния:
— взаимодействие осциллятора с
поглотителем. Состояние совокупной системы описывается тремя индексами ôа, с, wñ. Первый индекс указывает на состояние
атома, второй осциллятора, третий — стенок. Возможны три основные состояния:
1. ½1,0,0ñ
— атом возбужден, осциллятор в основном состоянии, стенки не возбуждены.
Энергия этого состояния системы равна энергии возбужденного атома ![]() .
. 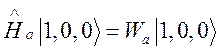 ,
, 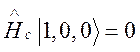 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.