2. ![]() — атом в нижнем состоянии с
— атом в нижнем состоянии с ![]() . Осциллятор в первом возбужденном
состоянии, стенки не возбуждены. Энергия этого состояния
. Осциллятор в первом возбужденном
состоянии, стенки не возбуждены. Энергия этого состояния ![]() , где
, где ![]() —
собственная частота резонатора.
—
собственная частота резонатора.
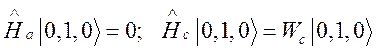 .
.
3. ![]() — атом в нижнем состоянии, осциллятор в
основном состоянии, стенки поглотили фотон с частотой
— атом в нижнем состоянии, осциллятор в
основном состоянии, стенки поглотили фотон с частотой ![]() . Энергия этого состояния
. Энергия этого состояния ![]() .
.
Волновую
функцию системы ![]() ищем в виде суперпозиции указанных
волновых функций:
ищем в виде суперпозиции указанных
волновых функций:
![]()
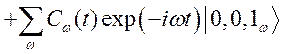 .
.
Поскольку стенки могут поглотить
любой фотон, то третье состояние является фактически набором состояний. Для
нахождения коэффициентов А(t), B(t) и ![]() решается
уравнение Шредингера методом теории возмущений:
решается
уравнение Шредингера методом теории возмущений:
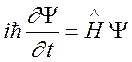 ,
(179)
,
(179)
где учитывается, что основные
волновые функции являются собственными функциями операторов ![]() и ортогональны между собой.
и ортогональны между собой.
В результате имеем
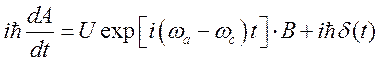 ;
;
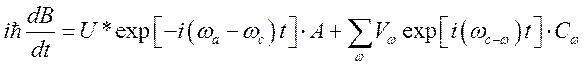 ; (180)
; (180)
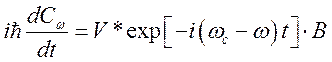 .
.
В этих уравнениях U и ![]() - матричные элементы операторов возмущений
- матричные элементы операторов возмущений
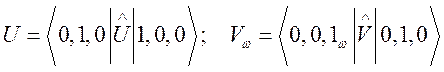 , (181)
, (181)
![]() —
учитывает начальное состояние системы, атом в возбужденном состоянии возникает
в момент времени t = 0.
—
учитывает начальное состояние системы, атом в возбужденном состоянии возникает
в момент времени t = 0.
Отметим, что
операторы ![]() не диагональны в выбранном представлении
не диагональны в выбранном представлении
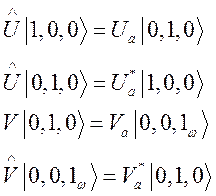 ;
(182)
;
(182)
Система (180) решается методом преобразования Лапласа. Не останавливаясь на деталях, рассмотрим результаты решения.
1 случай. Вначале рассмотрим частный случай
взаимодействия атома с континуумом осцилляторов поля свободного пространства.
Тогда ![]() и собственные значения
и собственные значения ![]() равны
равны ![]() ,
соответствующие плоским волнам c плотностью фотонов
,
соответствующие плоским волнам c плотностью фотонов ![]() с
волновым вектором
с
волновым вектором ![]() и поляризацией
и поляризацией ![]() . В волновой функции должен появиться
дополнительный совокупный индекс
. В волновой функции должен появиться
дополнительный совокупный индекс 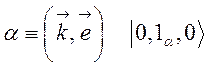 .
.
Предположим, что взаимодействие атома с полем дипольное
![]() .
.
Для вычисления матричных
элементов оператора взаимодействия ![]() используется стандартная
техника квантовой электродинамики (см. раздел 3.1), то есть поле разлагается в
ряд по плоским волнам (127). Задача вычисления
используется стандартная
техника квантовой электродинамики (см. раздел 3.1), то есть поле разлагается в
ряд по плоским волнам (127). Задача вычисления ![]() связана
с вычислением матричных элементов типа
связана
с вычислением матричных элементов типа 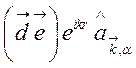 (см.
(138,139), где операторы
(см.
(138,139), где операторы ![]() , являясь коэффициентами
разложения поля (127), имеют матричные элементы, отличные от нуля только при
переходах, связанных с рождением для
, являясь коэффициентами
разложения поля (127), имеют матричные элементы, отличные от нуля только при
переходах, связанных с рождением для ![]() и гибели (для
и гибели (для ![]() ) фотонов (137).
) фотонов (137).
Окончательно имеем
![]() ;
;
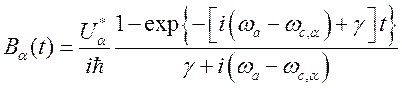 , (183)
, (183)
где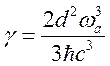 .
.
Вероятность
спонтанных переходов в единицу времени ![]() определяется
соотношением:
определяется
соотношением:
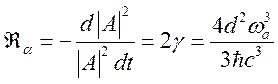 . (184)
. (184)
Распределение испущенных фотонов по частоте
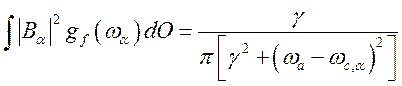 , (185)
, (185)
где![]() —
плотность состояний в пространстве.
—
плотность состояний в пространстве.
Таким образом, как вероятность излучений (184), так и ширина спектра (185) совпадают с полученными ранее (142,156).
2 случай. Затухание энергии в резонаторе A(t) = 0. (Атом не участвует в задаче). В начальный момент резонатор находится в первом возбужденном состоянии, а поглотитель (стенка) — в основном (не возбужденном) состоянии.
Решение системы (180) очевидно
![]() , (186)
, (186)
где
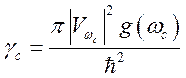 ,
,
![]() —
плотность состояний в поглотители,
—
плотность состояний в поглотители, ![]() — сдвиг частоты резонатора.
— сдвиг частоты резонатора.
Величина ![]() определяет добротность резонатора
определяет добротность резонатора 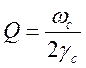 .
.
3 случай.
Скорость спонтанного распада атома в резонаторе. В задаче существует две
константы скорости: ![]() и
и ![]() , определяющие
затухание поля в резонаторе
, определяющие
затухание поля в резонаторе ![]() и распад атомной системы
и распад атомной системы
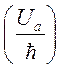 .
.
В
предположении 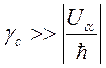 , из решения системы (180)
получим
, из решения системы (180)
получим
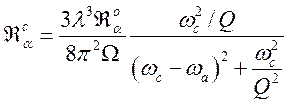 . (187)
. (187)
Видно, что при ![]() из (187) следует формула (177), то есть
вероятность возрастает в
из (187) следует формула (177), то есть
вероятность возрастает в ![]() раз
раз ![]() . Но из (187) так же следует, что при
наличии расстройки между
. Но из (187) так же следует, что при
наличии расстройки между ![]() и
и
![]() спонтанное излучение резонатора сильно
подавляется. Так, при
спонтанное излучение резонатора сильно
подавляется. Так, при ![]() вероятность уменьшается, по
сравнению с резонансным случаем, в
вероятность уменьшается, по
сравнению с резонансным случаем, в ![]() раз, а по сравнению с
вероятностью спонтанного излучения в свободном пространстве, в
раз, а по сравнению с
вероятностью спонтанного излучения в свободном пространстве, в ![]() раз
раз ![]() .
.
Спектр
излучения атома имеет лоренцовский профиль с шириной ![]() .
В противоположном случае
.
В противоположном случае 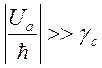 спектральное распределение
состоит из двух пиков с полушириной
спектральное распределение
состоит из двух пиков с полушириной ![]() , сдвинутых относительно
центра
, сдвинутых относительно
центра ![]() на расстояние
на расстояние 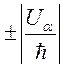 .
Физическая интерпретация этого явления состоит в том, что при
.
Физическая интерпретация этого явления состоит в том, что при 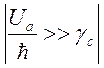 фотон, испущенный атомом, снова им
поглощается с большей вероятностью, чем стенкой. При
фотон, испущенный атомом, снова им
поглощается с большей вероятностью, чем стенкой. При ![]() связанная
система двух осцилляторов имеет два значения частот
связанная
система двух осцилляторов имеет два значения частот 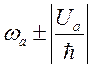 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.