В предыдущих разделах были рассмотрены основополагающие процессы взаимодействия излучения с веществом: поглощения, спонтанное и вынужденное излучение квантов света, а так же рассеяние фотонов.
Однако при увеличении интенсивности начинает играть важную роль множество других оптических процессов. Возбуждение и ионизация атома может осуществляться за счет одновременного поглощения двух и более фотонов. Пучок монохроматического света при взаимодействии с атомами может частично преобразовываться в свет, частоты которого являются гармониками основной частоты. С другой стороны, пучки с двумя и большим числом различных частот могут при взаимодействии создавать свет с частотой, равной сумме и разности исходных частот. Цель настоящего раздела – ознакомить читателя с некоторыми наиболее простыми и в то же время наиболее распространенными нелинейными процессами. Для более детального анализа можно рекомендовать литературу [4].
На языке
квантовой механики нелинейные процессы могут быть описаны членами высших
порядков при разложении вероятности перехода. В классической оптике нелинейные
процессы обусловлены сложной зависимостью вектора поляризации ![]() от интенсивности и частоты излучения.
Будем предполагать среду изотропной, а световые пучки одномодовыми, т.е.
имеющими заданные частоту и волновой вектор
от интенсивности и частоты излучения.
Будем предполагать среду изотропной, а световые пучки одномодовыми, т.е.
имеющими заданные частоту и волновой вектор ![]() .
.
Расчет
двухфотонного поглощения может быть проведен аналогично расчету сечения
рассеяния. Оба процесса обусловлены взаимодействием двух различных фотонов с
одним атомом. В рассматриваемом случае оба фотона поглощаются. Пусть фотоны
имеют различные частоты ![]() и
и ![]() и волновые векторы
и волновые векторы ![]() и
и
![]() . В результате поглощения атом переходит из
состояния i в состояние f.
Диаграммы трех возможных каналов процесса поглощения показаны на рис. 3
. В результате поглощения атом переходит из
состояния i в состояние f.
Диаграммы трех возможных каналов процесса поглощения показаны на рис. 3
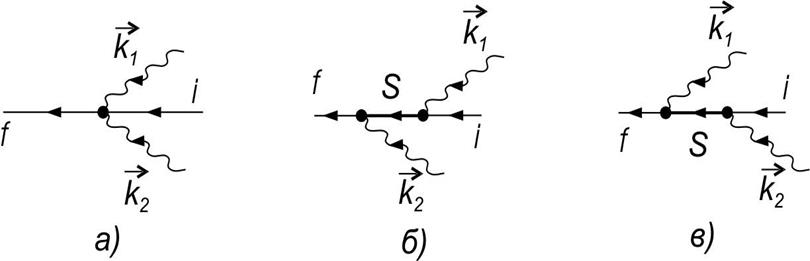

Отметим без
доказательств, что процесс, описанный диаграммой а) дает бесконечно
малый вклад в поглощение. Определяющую роль играют процессы б) и в),
в которых система из состояния i в состояние f переходит через одно или несколько промежуточных
состояний s. Отметим, что s – есть собственное состояние невозмущенного атома. Однако
при поглощении фотона с энергией ![]() возбуждение данного
состояния носит виртуальный характер. В формуле для вероятности перехода (4.1, 4.2)
учитывается только условие сохранения энергии во всем процессе, т.е.
возбуждение данного
состояния носит виртуальный характер. В формуле для вероятности перехода (4.1, 4.2)
учитывается только условие сохранения энергии во всем процессе, т.е. ![]() . В общем случае энергия промежуточного
состояния атома не равна энергии поглощенного кванта, т.е.
. В общем случае энергия промежуточного
состояния атома не равна энергии поглощенного кванта, т.е. ![]() , хотя для каждого такого состояния в
матричном элементе имеется сомножитель в знаменателе
, хотя для каждого такого состояния в
матричном элементе имеется сомножитель в знаменателе ![]() ,
уменьшающий вклад в матричный элемент состояний, энергия возбуждения которых
,
уменьшающий вклад в матричный элемент состояний, энергия возбуждения которых ![]() значительно отличается от энергии фотона
значительно отличается от энергии фотона ![]() . Система проходит через промежуточное
состояние s виртуально, закон сохранения энергии
не выполняется, т.к. в эти состояния нет реальных переходов.
. Система проходит через промежуточное
состояние s виртуально, закон сохранения энергии
не выполняется, т.к. в эти состояния нет реальных переходов.
Аналогично (1.15) для вероятности перехода
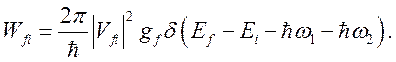 (5.1)
(5.1)
Здесь принято, что ![]() – число конечных состояний системы при
наличии одномодового монохроматического пучка равно
– число конечных состояний системы при
наличии одномодового монохроматического пучка равно ![]() –
статвесу атома.
–
статвесу атома.
Согласно (4.2), во втором порядке теории возмущений для диаграмм б) и в) имеем
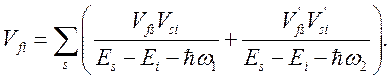 (5.2)
(5.2)
Ранее было показано (см. (2.9)), что
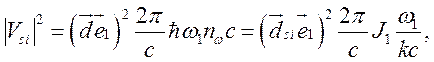 (5.3)
(5.3)
где ![]() –
дипольный момент,
–
дипольный момент, ![]() – вектор поляризации первого
фотона и
– вектор поляризации первого
фотона и ![]() – поток мощности излучения через единицу
поверхности. Учет (5.3) позволяет записать квадрат модуля матричного элемента
(5.2) в следующем виде:
– поток мощности излучения через единицу
поверхности. Учет (5.3) позволяет записать квадрат модуля матричного элемента
(5.2) в следующем виде:
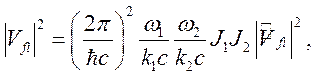 (5.4)
(5.4)
где
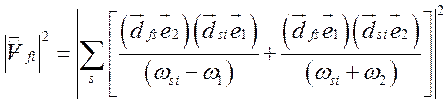 .
.
Наличие собственного времени жизни состояний i и f приводит к тому, что дельта-функция в (5.1) превращается в лоренцовскую функцию
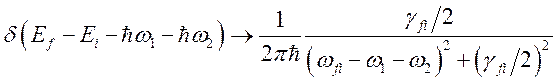 (5.5)
(5.5)
Окончательно из (5.1), (5.4) и (5.5) получим выражение для вероятности двухфотонного поглощения:
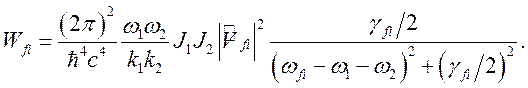 (5.6)
(5.6)
В выражении 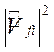 должно быть проведено усреднение по
ориентациям атомов относительно поляризации световых пучков. Это дает
дополнительный числовой множитель и не повлияет на общий характер зависимости
вероятности
должно быть проведено усреднение по
ориентациям атомов относительно поляризации световых пучков. Это дает
дополнительный числовой множитель и не повлияет на общий характер зависимости
вероятности ![]() от основных параметров. Поэтому мы здесь
этого делать не будем.
от основных параметров. Поэтому мы здесь
этого делать не будем.
Волновые
векторы ![]() и
и ![]() связаны
с частотами
связаны
с частотами ![]() и
и ![]() обычным
уравнением
обычным
уравнением
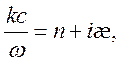 (5.7)
(5.7)
где n
и ![]() –
действительная и мнимая часть показателя преломления. Мнимой частью
–
действительная и мнимая часть показателя преломления. Мнимой частью ![]() можно пренебречь, если в
исследуемой среде отсутствуют поглощение на частотах
можно пренебречь, если в
исследуемой среде отсутствуют поглощение на частотах ![]() и
и
![]() . Однако показатель преломления в общем
случае может отличаться от единицы.
. Однако показатель преломления в общем
случае может отличаться от единицы.
Вероятность двухфотонного перехода может быть использована для нахождения характеристик распространения двух световых пучков через среду, состоящую из одинаковых атомов. Допустим, что два пучка распространяются вдоль оси x. Тогда переход атомов с состояние f в некоторой точке x описывается выражением
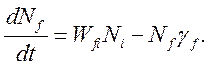 (5.8)
(5.8)
Здесь ![]() – концентрация
атомов в единице объема.
– концентрация
атомов в единице объема.
Поглощаемая мощность для каждого пучка (пучки предположим квазистационарными):
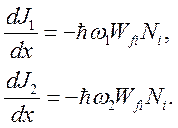 (5.9)
(5.9)
Откуда 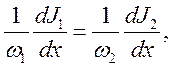 т.е.
т.е.
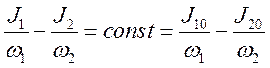 .
.
Это соотношение отражает тот простой факт, что в каждом акте поглощения каждый световой пучок теряет по одному фотону.
Теперь можно в
(5.9) разделить систему на уравнения для ![]() и
и ![]() , решение которых имеет вид
, решение которых имеет вид
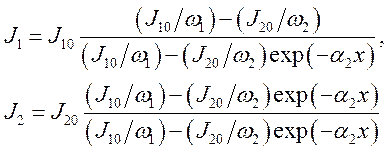 (5.10)
(5.10)
где коэффициент двухфотонного
поглощения ![]() определяется выражением
определяется выражением
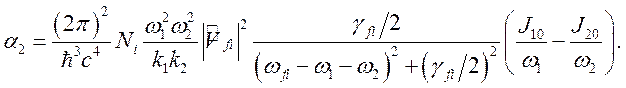 (5.11)
(5.11)
Предполагалось, что первый пучок
фотонов больше, чем второй. ![]() и число атомов в
начальном состоянии
и число атомов в
начальном состоянии ![]() не изменялось, т.е. двухфотонное
поглощение мало.
не изменялось, т.е. двухфотонное
поглощение мало.
Приведенное
решение остается в силе и при равенстве потоков фотонов. Однако, когда ![]() , то экспоненциальная зависимость в (5.10)
заменяется зависимостью
, то экспоненциальная зависимость в (5.10)
заменяется зависимостью ![]() .
.
Во многих
экспериментах один пучок с фиксированной частотой ![]() создается
мощным лазером, а второй, слабый создается источником с переменной (регулируемой)
частотой, что позволяет настраиваться на резонанс
создается
мощным лазером, а второй, слабый создается источником с переменной (регулируемой)
частотой, что позволяет настраиваться на резонанс ![]() . В
этом случае изменение интенсивности пучка
. В
этом случае изменение интенсивности пучка ![]() невелико,
т.е.
невелико,
т.е. ![]() , а для
, а для ![]() имеем
имеем ![]() . Поведение второго пучка сходно с обычным
поглощением.
. Поведение второго пучка сходно с обычным
поглощением.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.