Нелинейная оптика (Глава 5 учебного пособия), страница 2

При выводе уравнения для вероятности перехода в случае неупругого рассеяния света атомом предполагалось, что падающий пучок имел определенное число фотонов, а до рассматриваемого акта рассеянных фотонов не было.

Такое же вычисление нетрудно провести для более общего случая, когда рассеянные фотоны есть. В этом случае математическая запись вероятности такого процесса аналогична двухфотонному поглощению (см. (5.6)), только смысл матричных элементов другой.

Если  — средняя интенсивность падающего и  — рассеянного излучения, то, аналогично (5.9), получим

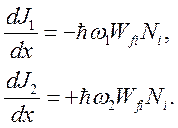                                               (5.12)

Здесь для простоты предполагалось, что рассеянное излучение имеет только одну моду. В общем случае число рассеянных мод определяется условиями усиления и конфигурации возбужденной среды  аналогично (5.6). Из (5.12) получим

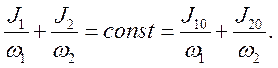
Таким образом, полный поток фотонов сохраняется: каждый фотон, потерянный падающим пучком, компенсируется фотоном рассеянным.

Не будем останавливаться на деталях решения системы уравнений (5.12) с учетом линейной зависимости  от интенсивностей. Выпишем лишь выражения для  при следующем предположении: начальный поток рассеянных фотонов определяется спонтанным излучением одного кванта , где V – объем рассеяния. Если , то , т.е. интенсивность растет линейно с расстоянием.

В противоположном случае , , т.е. весь поток падающих фотонов превращается в поток рассеянных фотонов.

И в промежуточном случае  интенсивность рассеянного пучка возрастает экспоненциально:

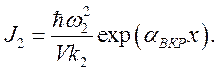
Здесь  получается из выражения для  (5.11) заменой  на .

5.3. Генерация третьей гармоники и КАРС

В случае генерации третьей гармоники в одном акте взаимодействия требуется уничтожить три фотона с частотой  и создать один фотон с частотой . Всего здесь имеется четыре электрических дипольных взаимодействия, т.е. необходима теория возмущений четвертого порядка:

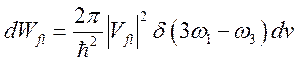                                  (5.13)

и

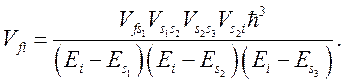
Здесь матричные элементы находятся аналогично изложенному в разделе 2.2. Однако вероятность перехода при генерации третьей гармоники обнаруживает новое свойство, которым не обладают скорости двухфотонного поглощения и вынужденное рассеяние [4]. После окончания двух последних процессов атом остается в конкретном конечном состоянии, и каждый отдельный переход приводит к возбуждению определенного атома. Координатная зависимость электромагнитного поля (4.3) вычисляется в точке нахождения атома. Поэтому полная скорость перехода равна сумме скоростей переходов для отдельных атомов, а коэффициент поглощения пропорционален числу атомов  (5.11).

Скорость генерации гармоник ведет себя иначе. Поскольку в этом случае конечное состояние f совпадает с начальным i(f = i), то нет различия между переходами, происходящими с различными атомами. Следовательно, матричный элемент должен быть просуммирован по всем вкладам различных атомов до того, как он будет возведен в квадрат для получения полной скорости перехода. Это означает, что учет числа атомов проводится не на стадии записи уравнения типа (5.9), а при расчете вероятности W.